A menudo, la física teórica nos desafía con conceptos que parecen sacados de una novela de ciencia ficción. Pero, ¿qué pasaría si te dijéramos que las partículas que conocemos—fermiones y bosones—no son las únicas formas posibles de materia? Un reciente estudio publicado en Nature por Zhiyuan Wang y Kaden Hazzard propone algo extraordinario: la existencia de “parapartículas”, partículas que no encajan en ninguna de estas categorías tradicionales. La física de partículas podría dar un vuelco.
Aunque la idea de partículas más allá de los fermiones y bosones no es nueva, siempre se consideró poco más que una curiosidad matemática. Sin embargo, el reciente artículo no solo revive este concepto, sino que lo valida matemáticamente en ciertos sistemas físicos.
Una breve historia: fermiones, bosones y el origen de las parapartículas
Para comprender la importancia de este avance, necesitamos repasar la clasificación estándar de las partículas. Desde las primeras formulaciones de la mecánica cuántica, las partículas se agrupan en fermiones y bosones según sus comportamientos estadísticos. Los fermiones obedecen el principio de exclusión de Pauli, lo que significa que dos partículas no pueden ocupar el mismo estado cuántico. Este principio es el responsable de la estructura de la tabla periódica y de fenómenos tan comunes como la solidez de los materiales. Los bosones, por otro lado, pueden compartir el mismo estado cuántico, lo que hace posible fenómenos como la condensación de Bose-Einstein.
La pregunta sobre si podrían existir partículas fuera de estas categorías no es nueva. Greenberg y Messiah exploraron esta posibilidad en 1965, introduciendo el concepto de parapartículas, que exhibirían combinaciones intermedias de simetría entre fermiones y bosones. Sin embargo, estos conceptos fueron considerados como curiosidades matemáticas sin relevancia física concreta. Esto cambió en los años 70, cuando algunos estudios demostraron que, bajo ciertas condiciones, las parapartículas parecían indistinguibles de fermiones o bosones. La investigación de Wang y Hazzard se contrapone a esta suposición al identificar un marco matemático en el que las parapartículas pueden surgir con propiedades observables únicas.
En particular, Hartle y Taylor, en 1969, examinaron cómo estas partículas pueden ser compatibles con la mecánica cuántica si se cumple la ley de clúster, que exige que sistemas suficientemente separados no interfieran entre sí. Estos estudios establecieron las bases para que trabajos posteriores exploraran las condiciones bajo las cuales las parapartículas podrían tener un impacto observable.

El avance reciente: matemáticas complejas y física condensada
En su artículo de 2025, Wang y Hazzard proponen un marco teórico basado en álgebras de Lie, la ecuación de Yang-Baxter y otras herramientas matemáticas avanzadas. Este enfoque les ha permitido formular una teoría generalizada de “parastadísticas” aplicable a sistemas físicos específicos. Según sus cálculos, las parapartículas pueden surgir como cuasi-partículas en sistemas de materia condensada, como ciertos modelos de espines cuánticos.
Lo más notable es que estas partículas presentan características únicas en comparación con los fermiones y bosones. Cuando se intercambian entre sí, sus estados internos cambian de forma compleja, algo que no ocurre con las partículas tradicionales. Esto implica que su dinámica y estadística podrían conducir a propiedades novedosas en materiales y aplicaciones tecnológicas.
Por otra parte, este descubrimiento podría tener implicaciones prácticas, especialmente en el campo de la información cuántica, mediante la manipulación de sus estados internos. Aunque todavía estamos lejos de aplicaciones concretas, las posibilidades son intrigantes.
Para ejemplificar este avance, los investigadores utilizaron modelos de sistemas cuánticos en dos dimensiones. Estos modelos son cruciales porque permiten observar directamente cómo las parapartículas se comportan como excitaciones dentro de materiales condensados. De manera especial, se enfocaron en sistemas de espines cuánticos, donde las partículas exhiben exclusión estadística generalizada y propiedades de intercambio nunca vistas antes.

Una red cuántica para estudiar las parapartículas
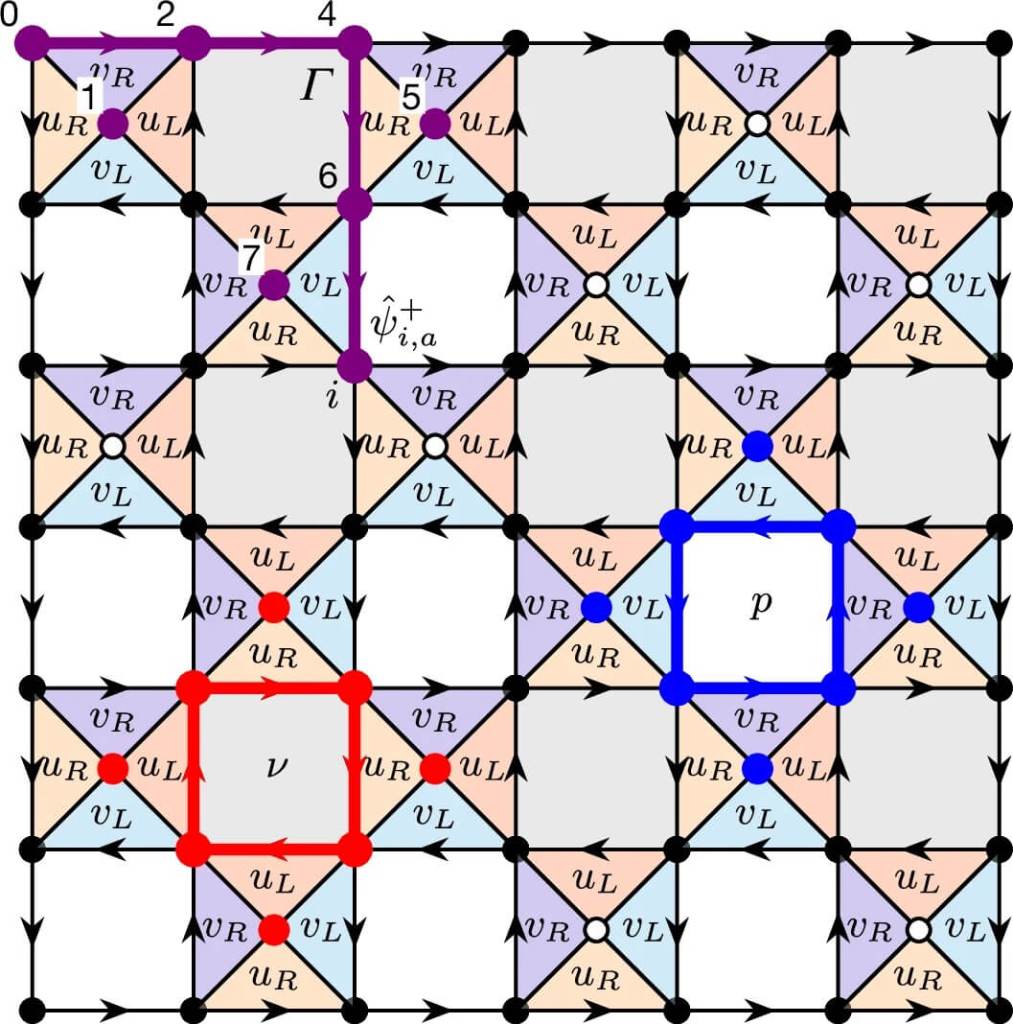
Un elemento clave en el estudio de las parapartículas es el uso de redes cuánticas como la representada en la figura. En esta red, cada punto negro corresponde a un qudit de 16 dimensiones, mientras que los círculos abiertos representan qudits auxiliares de 64 dimensiones. Los triángulos coloreados indican interacciones de tres cuerpos entre los qudits en sus vértices, y las plaquetas blancas y grises muestran interacciones de ocho cuerpos. Por otra parte, la línea púrpura muestra un operador de parapartícula que actúa de manera consecutiva sobre los puntos que recorre, permitiendo modelar las propiedades estadísticas y dinámicas únicas de estas partículas.
Un qudit es la generalización de un qubit en computación cuántica, que puede existir en más de dos estados, algo que permite representar información cuántica en sistemas con dimensiones superiores a las binarias.
Enraizando el presente en el pasado: revisitando los fundamentos
El marco teórico de Wang y Hazzard se inspira en estudios previos que exploraron la naturaleza de las simetrías y permutaciones en sistemas de partículas. Por ejemplo, en 1970, Stolt y Taylor clasificaron a las parapartículas en dos grandes familias: parabosones y parafermiones. Estas categorías, a su vez, se dividen en órdenes específicos según sus propiedades de simetría. En sus conclusiones, argumentaron que si bien las parapartículas pueden surgir matemáticamente, su observación directa sería extremadamente difícil sin un marco experimental apropiado.
Este tipo de reflexiones sirve para entender mejor el progreso actual. Los avances matemáticos recientes han superado algunas de las limitaciones que anteriormente dificultaban la validación experimental de estos conceptos. Al conectar estas ideas con sistemas de materia condensada, los investigadores actuales han encontrado un puente entre la abstracción matemática y las posibles aplicaciones físicas.
Referencias
- J.B. Hartle, J.R. Taylor, Quantum Mechanics of Paraparticles. Physical Review, 178, 2043 (1969). DOI: 10.1103/PhysRev.178.2043
- R.H. Stolt, J.R. Taylor, Classification of Paraparticles. Physical Review D, 1, 2226 (1970). DOI: 10.1103/PhysRevD.1.2226
- Zhiyuan Wang, Kaden R.A. Hazzard, Particle exchange statistics beyond fermions and bosons. Nature, 2025. DOI: 10.1038/s41586-024-08262-7
Cortesía de Muy Interesante
Dejanos un comentario: