En los últimos años, la unión entre la luz y la topología ha abierto nuevas fronteras en la física cuántica, con aplicaciones que podrían transformar nuestra tecnología. Desde materiales que conducen electricidad de manera insólita hasta partículas que parecen moverse en dimensiones ocultas, la ciencia está redescubriendo cómo funciona el mundo en sus niveles más fundamentales. Un reciente artículo, titulado “Interacting topological quantum aspects with light and geometrical functions”, nos lleva un paso más allá. En este trabajo, Karyn Le Hur explora cómo la luz y los efectos geométricos pueden caracterizar propiedades topológicas en sistemas cuánticos.
Lo que hace que este estudio sea fascinante es cómo logra conectar conceptos aparentemente abstractos, como la geometría de la esfera de Bloch, con fenómenos concretos como la respuesta a la luz polarizada circularmente. Este enfoque ofrece herramientas prácticas para desarrollar materiales y dispositivos innovadores.
Topología en la esfera de Bloch: una herramienta para entender la materia cuántica
La esfera de Bloch es una representación geométrica que permite visualizar el estado de un sistema cuántico de dos niveles, como el de un electrón que tiene dos posibles estados de spin. En este estudio, Le Hur utiliza un enfoque basado en campos magnéticos radiales, los cuales generan estructuras topológicas denominadas “Skyrmiones“. Estas estructuras emergen como resultado de un campo magnético radial aplicado al sistema, y su presencia puede detectarse mediante la interacción con luz polarizada circularmente.
En términos prácticos, esto significa que se pueden medir propiedades topológicas globales —como el “número de Chern”— observando cómo el sistema responde a la luz. Este número de Chern es una cantidad que describe cuántas veces el sistema “envuelve” ciertos puntos críticos en el espacio, lo que se relaciona directamente con propiedades como la conductividad eléctrica en materiales especiales.
Un aspecto fascinante de este modelo es cómo relaciona conceptos clásicos y cuánticos. En este sentido, Le Hur demuestra que las propiedades topológicas de la esfera de Bloch pueden reescribirse en términos de los polos norte y sur de la esfera, lo que simplifica la descripción de estos sistemas y su interacción con luz.
Respuestas ópticas y el efecto fotoeléctrico topológico
Uno de los puntos más destacados del artículo es cómo la luz polarizada circularmente puede utilizarse para revelar las propiedades topológicas de un sistema. Al incidir con luz en un material, las partículas responden de maneras predecibles dependiendo de las características topológicas del sistema. En este caso, Le Hur muestra que la respuesta óptica no solo está cuantificada, sino que está protegida por las propiedades topológicas del sistema, lo que la hace extremadamente robusta frente a perturbaciones externas.
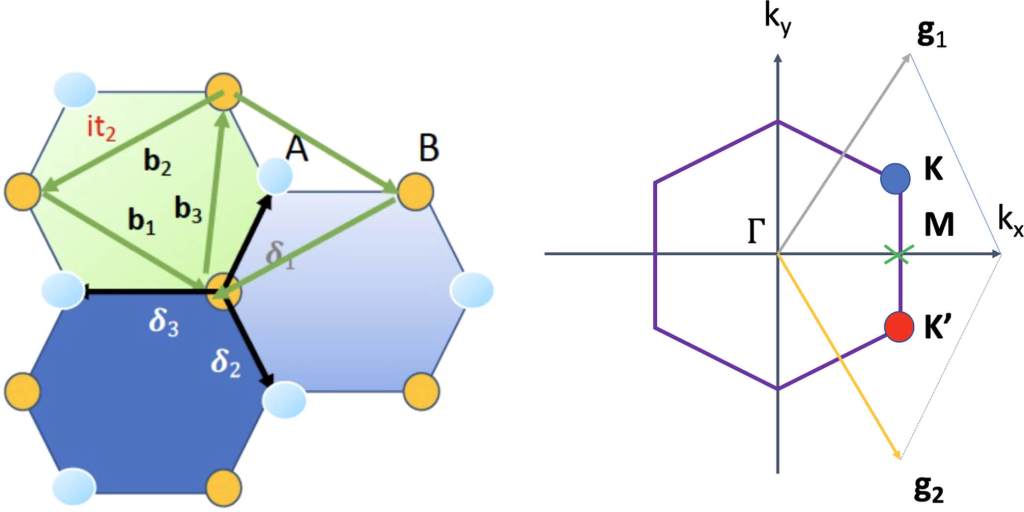
En un material como el grafeno, que tiene una estructura de red hexagonal, se puede observar un “efecto fotoeléctrico topológico” cuando la luz excita electrones de manera controlada. Estos fenómenos se relacionan con las interacciones entre la luz y los llamados puntos de Dirac en el material, donde la energía de los electrones presenta un comportamiento cónico. Este efecto abre posibilidades en el diseño de dispositivos que puedan manipular corrientes eléctricas mediante luz.

Aplicaciones en materiales topológicos y computación cuántica
Más allá de las aplicaciones ópticas, el trabajo también tiene implicaciones en el diseño de nuevos materiales cuánticos. Sistemas como los aislantes topológicos y los semimetales de Weyl presentan propiedades electrónicas únicas que podrían ser utilizadas en dispositivos electrónicos del futuro. Por otra parte, este enfoque geométrico permite explorar estados cuánticos exóticos, como los fermiones de Majorana, que tienen aplicaciones prometedoras en la computación cuántica.
Un aspecto notable del estudio es su capacidad para describir interacciones complejas mediante un enfoque local en el espacio de momentos. Esto permite extender el análisis a sistemas más realistas, como materiales con desorden o interacciones fuertes entre partículas. El enfoque se ha aplicado al modelo de Haldane, un sistema prototípico en la física de materiales topológicos, permitiendo identificar transiciones entre fases topológicas y fases “Mott” altamente correlacionadas.
Resumen para gente sin tiempo
Los científicos están investigando cómo ciertos materiales reaccionan a la luz para descubrir secretos que no son visibles a simple vista. Cuando estos materiales interactúan con luz especial, como la luz polarizada (que vibra en una dirección concreta o en espiral), las partículas dentro de ellos se comportan de formas únicas que ayudan a entender mejor su estructura.
Materiales → Luz polarizada → Comportamiento único de partículas (explicado con topología) → Aplicaciones
Todo esto tiene que ver con algo llamado topología, que básicamente es una manera de estudiar cómo están organizadas las partes de un material. Es como analizar un rompecabezas para entender cómo encajan sus piezas, pero en este caso, ocurre a nivel atómico. Gracias a estas observaciones, los científicos pueden comprender mejor cómo funcionan estos materiales desde dentro.

Referencias
- Karyn Le Hur. “Interacting topological quantum aspects with light and geometrical functions”. Physics Reports 1104 (2025): 1–42. DOI: 10.1016/j.physrep.2024.11.003
Cortesía de Muy Interesante
Dejanos un comentario: