La física cuántica es una fuente constante de desafíos de nuestra intuición. Uno de los desarrollos más emocionantes en este campo es el de las redes cuánticas, sistemas que conectan computadoras cuánticas para transmitir información de manera ultra segura y rápida. Sin embargo, estas redes se enfrentan a un problema crítico: su inestabilidad natural, ya que las conexiones que las sostienen se destruyen después de cada uso.
Un equipo de investigadores liderado por István Kovács de la Universidad Northwestern ha hecho un descubrimiento fascinante que podría transformar este panorama. Publicado en Physical Review Letters, el estudio demuestra que es posible mantener estas redes funcionales mediante una estrategia eficiente: añadir un “número mágico” de enlaces después de cada comunicación. Este número, que crece con la raíz cuadrada del número de usuarios, permite evitar el colapso de la red con recursos mínimos.
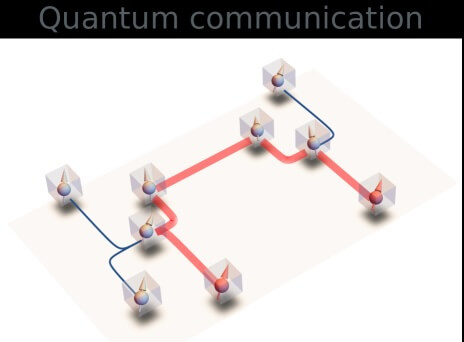
El desafío de las redes cuánticas explicado con islas y puentes
Para entender cómo funcionan estas redes, podemos imaginarlas como una ciudad formada por islas conectadas por puentes. Las islas representan a los usuarios (como computadoras cuánticas), y los puentes son las conexiones que permiten transmitir información. Cada vez que alguien cruza un puente, este se destruye tras el uso, dejando menos conexiones disponibles.
Esta fragilidad se debe a una característica única de la comunicación cuántica: el entrelazamiento cuántico, el recurso que permite que dos partículas “hablen” entre sí de manera instantánea, incluso a grandes distancias. Según el estudio, “cada comunicación de 1 qubit elimina todos los enlaces participantes en el camino de comunicación”. Si no se reconstruyen nuevos puentes, las islas quedan aisladas y la red colapsa.
El hallazgo del número mágico
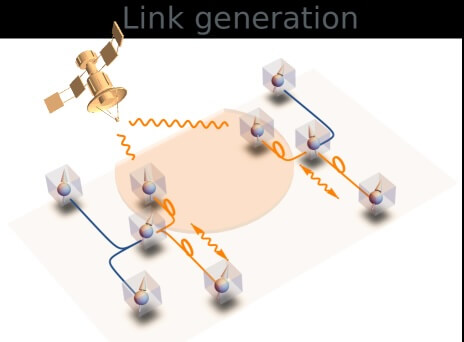
El equipo de investigadores encontró que no es necesario reconstruir todos los puentes destruidos, lo cual sería ineficiente y costoso. En su lugar, basta con añadir un pequeño número de enlaces nuevos, calculado como la raíz cuadrada del total de usuarios de la red.
Por ejemplo:
- Para una red con 1.000 usuarios, se necesitan solo 32 enlaces nuevos para mantenerla estable.
- En una red más grande, con 1.000.000 de usuarios, bastan 1.000 enlaces nuevos.
Esto significa que, aunque el número de usuarios crezca enormemente, el número de nuevas conexiones necesarias aumenta mucho más lentamente. Esta relación se puede expresar con una fórmula sencilla:
Donde:
- α* es el número mágico de enlaces necesarios.
- N es el número total de usuarios en la red.
Gracias a esta fórmula, sabemos exactamente cuántas conexiones hay que añadir para mantener la estabilidad de la red, sin malgastar recursos.
Este enfoque permite ahorrar recursos sin comprometer la funcionalidad de la red. Como señala el estudio, “el número crítico de enlaces escala con la raíz cuadrada del tamaño de la red, lo que resulta en un sistema sorprendentemente eficiente”.
¿Por qué este descubrimiento es tan relevante?
Además de su eficiencia, esta estrategia tiene implicaciones profundas para el desarrollo del internet cuántico, una red global de computadoras cuánticas que promete comunicaciones ultrarrápidas y seguras. Resolver la fragilidad de las redes es un paso clave para hacer realidad esta tecnología revolucionaria.
Cómo se comportan las redes cuánticas bajo presión
El artículo también describe cómo las redes cuánticas colapsan en ausencia de una estrategia de mantenimiento. Según los autores, una red típica sin reposición de enlaces se desintegra rápidamente, especialmente si es pequeña o está basada en tecnologías como fibras ópticas.
En las simulaciones realizadas, los investigadores analizaron diferentes tipos de redes y descubrieron que, sin mantenimiento, incluso las redes más robustas pierden su capacidad de conectar usuarios tras pocos eventos de comunicación. Esto pone en evidencia la urgencia de una solución práctica como la que propone este estudio.
Un aspecto sorprendente del hallazgo es que la estructura inicial de la red no afecta al resultado final: con el número adecuado de enlaces añadidos, todas las redes convergen hacia un estado estable y funcional. Esto las hace más flexibles para ser implementadas en diferentes escenarios tecnológicos, como satélites o fibra óptica.
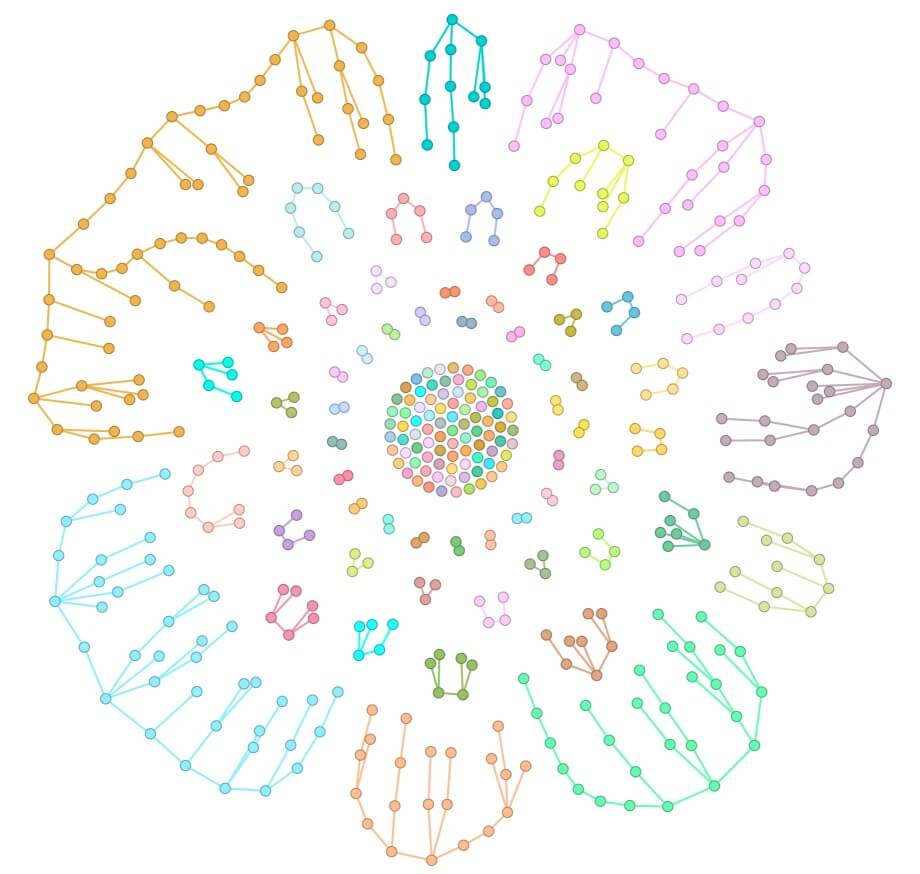
Las topologías de red cuántica: cómo su estructura afecta la estabilidad
El diseño de una red cuántica no solo depende de las conexiones entre sus nodos, sino también de su topología inicial, es decir, cómo están organizados los nodos y enlaces desde el principio. Esto es clave porque la estructura de la red influye directamente en su capacidad para mantenerse funcional cuando los enlaces se destruyen y deben regenerarse.
Las redes cuánticas pueden configurarse de diversas maneras, y cada topología tiene ventajas y desventajas dependiendo del uso y los recursos disponibles.
1. Árboles y redes de panal bidimensional (2D Hex)
En topologías como los árboles y los panales bidimensionales, los nodos están conectados de manera ordenada, pero con pocas redundancias. Esto las hace eficientes en términos de recursos, pero también las vuelve altamente frágiles. Si un enlace crucial se destruye, es probable que una parte importante de la red quede desconectada.
2. Redes Erdős-Rényi (ER)
En estas redes, las conexiones entre nodos se distribuyen de manera aleatoria, lo que introduce un cierto grado de redundancia. Esto permite que sean más robustas que los árboles o los panales, pero su estabilidad sigue siendo limitadasi no se regeneran enlaces rápidamente tras las comunicaciones.
3. Redes completas
En un gráfico completo, todos los nodos están conectados entre sí. Aunque esta configuración es la más robusta, ya que ofrece múltiples caminos alternativos para mantener la comunicación, también es extremadamente costosa en términos de recursos.
La importancia de la regeneración
Independientemente de la topología inicial, todas las redes cuánticas colapsan con el tiempo si no se regeneran los enlaces. Como se muestra en simulaciones del estudio, las redes menos conectadas (como los árboles) tienden a desintegrarse en pocos pasos de tiempo, mientras que una red completa puede sobrevivir más tiempo antes de fallar.
El futuro del internet cuántico: hacia redes más seguras y eficientes
El internet cuántico promete revolucionar la comunicación en muchos aspectos, desde transacciones bancarias ultra seguras hasta nuevos métodos de colaboración científica. Sin embargo, su implementación a gran escala depende de resolver desafíos técnicos, como el que aborda este estudio.
La clave del avance radica en el diseño de estrategias de mantenimiento automáticas. Por ejemplo, las redes podrían programarse para añadir enlaces automáticamente cuando detecten que otros se han destruido. Esto no solo asegura la estabilidad, sino que también mejora la eficiencia al evitar la reconstrucción innecesaria de enlaces redundantes.
Como señala Kovács en el estudio: “El diseño estratégico de las redes cuánticas puede permitir que alcancen su máximo potencial, superando las limitaciones que encontramos en las redes clásicas”.
Referencias
- Xiangyi Meng, Bingjie Hao, Balázs Ráth, István A. Kovács. Path Percolation in Quantum Communication Networks. Physical Review Letters, 23 de enero de 2025. DOI: 10.1103/PhysRevLett.134.030803
Cortesía de Muy Interesante
Dejanos un comentario: