Menos desperdicio, más beneficio: optimización matemática en la industria

¿Has observado alguna vez cuánto material se desperdicia al cortar papel para un proyecto escolar o te has planteado el problema de acomodar todas las maletas en el maletero de tu coche? En la industria, estos problemas de optimización espacial se multiplican exponencialmente, con importantes consecuencias económicas y ambientales.

1. Introducción: el reto de aprovechar cada centímetro

Las empresas fabricantes de vidrio se enfrentan diariamente al desafío de cortar grandes láminas de vidrio, de aproximadamente 6×3 metros, para satisfacer los pedidos de clientes que necesitan piezas de diferentes tamaños. Cada centímetro desperdiciado representa no solo una pérdida económica sino también un impacto ambiental, pues la fabricación de vidrio consume grandes cantidades de energía y materias primas.

La optimización del corte puede suponer para una empresa mediana un ahorro de miles de euros y toneladas de material anualmente. Aunque tradicionalmente este problema se abordaba con reglas prácticas y experiencia, hoy los algoritmos matemáticos ofrecen soluciones mucho más eficientes en segundos.

2. El problema: un rompecabezas con reglas especiales

Del horno a la ventana: el viaje del vidrio plano

El vidrio plano se fabrica con una mezcla de arena de sílice, ceniza de sosa, piedra caliza y dolomita que se funde en hornos a temperaturas extremas de 1550°C. Esta masa líquida se extiende sobre un baño de estaño fundido formando una cinta continua que, al enfriarse, se solidifica y se corta en grandes láminas. El proceso aparece en la Figura 1. 

Estas láminas no son perfectas: durante el proceso de fabricación pueden aparecer pequeñas burbujas o imperfecciones que son detectadas por escáneres de alta precisión. Esto hace que cada lámina sea única y se haya que determinar un patrón de corte específico para cada una. La Figura 2 da una idea de la escala industrial del proceso.

El arte de cortar vidrio: limitaciones técnicas

El vidrio impone restricciones particulares sobre la forma en la que puede ser cortado debido a su naturaleza:

• Solo permite cortes rectos de lado a lado (llamados “cortes de guillotina”), que dividen un rectángulo en dos nuevos rectángulos. No se pueden realizar cortes curvos o cortes que no atraviesen completamente el rectángulo.
• El proceso se realiza en tres etapas: primero cortes verticales para crear tiras, luego horizontales para formar rectángulos y finalmente verticales otra vez para obtener las piezas finales. 
• Los defectos deben quedar en las zonas de desecho, nunca en las piezas finales, ya que podrían comprometer su integridad estructural o apariencia estética.
• Las piezas pueden rotarse 90° para aprovechar mejor el espacio, pero las láminas originales siempre mantienen su orientación horizontal.
• Existen restricciones técnicas adicionales, como distancias mínimas entre cortes para evitar roturas no deseadas o áreas mínimas de desecho para facilitar la manipulación de los fragmentos.

El proceso de corte paso a paso

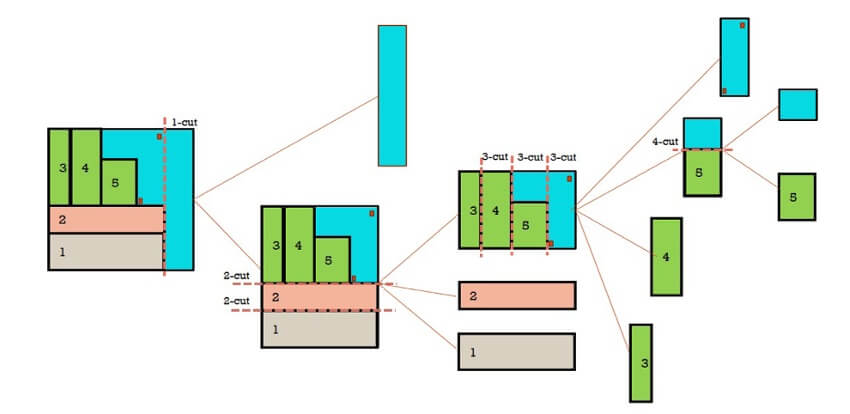
La Figura 3 muestra cómo funciona este proceso. Las piezas que necesitamos obtener aparecen en colores, mientras que los defectos son los pequeños rectángulos rojos que debemos evitar. El proceso sigue una secuencia fija:

1. Primer corte (vertical): Divide la lámina en tiras verticales. En este ejemplo, el primer corte crea dos tiras, una a la derecha que es desecho (en azul) y otra a la izquierda de la que se cortarán las piezas.
2. Segundo corte (horizontal): Divide la tira vertical de la izquierda en tiras horizontales. Aquí se obtienen las piezas 1 y 2, y queda un rectángulo en la parte superior que se puede seguir cortando.
3. Tercer corte (vertical):   Crea tiras verticales para obtener las piezas finales. Este corte separa las piezas 3 y 4, crea una tira de desecho a la derecha y otra tira de la cual se puede obtener la pieza 6 mediante un recorte final para obtener la pieza conocida como trimming.

Un aspecto importante es que el último rectángulo de desecho obtenido en el primer corte no se contaría como pérdida si esta fuera la última lámina utilizada, ya que podría reutilizarse en procesos posteriores.

3. La solución: un sistema inteligente de selección de patrones

Para resolver este complejo problema, hemos desarrollado un sistema que funciona como un jugador de ajedrez planificando su estrategia: analiza múltiples posibilidades, evalúa sus consecuencias y selecciona las más prometedoras.

La evolución de estos algoritmos refleja no solo avances matemáticos, sino también la creciente capacidad de cómputo disponible. Problemas que hace veinte años requerían supercomputadoras ahora pueden resolverse en un ordenador portátil estándar, y con mejores resultados.

¿Cómo funciona nuestro sistema de búsqueda en haz?

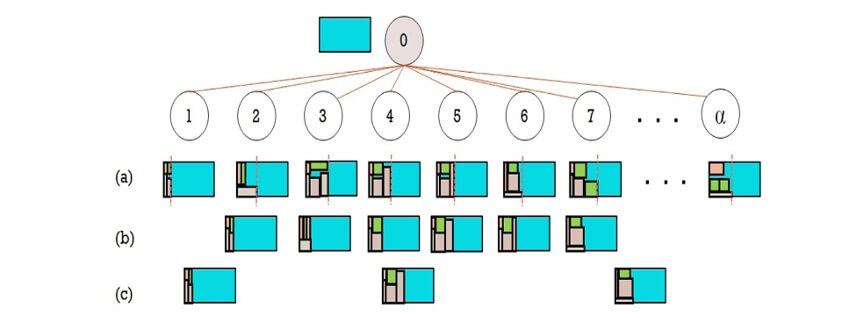
El algoritmo está basado en un método llamado “búsqueda en haz” (Beam Search), que utiliza una estructura de árbol para construir buenas soluciones.  El nodo raíz es una solución vacía y cada nivel posterior se define en un proceso en dos fases, una fase constructiva y una fase de evaluación.

1.- Fase constructiva

A la solución del nodo del nivel anterior, añade una tira vertical (como la tira de la izquierda de la primera etapa de la Figura 3). Esto puede hacerse de muchas maneras, pudiendo producir muchos nodos sucesores.  Para ello, ha de tomar estas decisiones:

1. Qué espacio vacío utilizar primero: Generalmente, comienza por el que está más a la izquierda y más abajo, pero adapta esta regla según los defectos presentes y el estado de corte.
2. Qué pieza colocar: Prioriza diferentes criterios según la etapa de corte. En las primeras etapas suele seleccionar las piezas más anchas o más grandes, mientras que en etapas posteriores puede usar otros criterios para adaptarse al espacio vacío disponible.
3. Dónde colocarla exactamente: Determina la posición óptima para cada pieza, evitando defectos y maximizando el aprovechamiento del espacio disponible.

Introduce variedad controlada: El proceso constructivo incorpora cierto grado de aleatorización, en la selección de la pieza y de su posición, para evitar soluciones repetitivas y descubrir patrones innovadores que podrían pasar desapercibidos. 

2.- Fase de evaluación

Para que el árbol de búsqueda no crezca de forma exponencial, un proceso de evaluación de las soluciones obtenidas en la fase de construcción reduce su número, de forma que solo se mantiene una parte, un haz de nodos, para formar el siguiente nivel del árbol. Se realiza mediante una doble evaluación: una evaluación local rápida, que se aplica a todas las soluciones de la fase constructiva, y una evaluación global, más lenta, que solo se aplica a las que obtienen mejores resultados en la evaluación local.

El algoritmo depende de tres parámetros. El primero, α, determina el número de soluciones de la fase constructiva, generadas a partir de cada nodo del nivel anterior. El valor de α depende del tamaño del problema y del nivel de ramificación. Todas estas soluciones se evalúan localmente, utilizando como criterio el porcentaje de ocupación del espacio. El segundo parámetro, β (amplitud de filtro), determina el número de soluciones que van a la evaluación global, que consiste en completar la solución parcial hasta llegar a una solución completa. El tercer parámetro, 𝛾 (amplitud del haz), determina el número de nodos que se mantienen en cada nivel. 

La Figura 4 ilustra el proceso. Comenzando desde una solución vacía en el nodo raíz, para formar el primer nivel se construyen α soluciones parciales, formadas por una tira vertical. En el segundo paso, la evaluación local selecciona los β mejores nodos (β =6 en la figura). En el tercer paso, los 𝛾 nodos más prometedores se mantienen para continuar construyendo las soluciones (𝛾 =3 en la figura). Por tanto, el nuevo nivel del árbol estará formado por esos tres nodos, y el proceso se repite a partir de cada nuevo nodo hasta conseguir soluciones completas en las que se corten todas las piezas demandadas.

Este sistema puede analizar millones de combinaciones de corte en segundos, algo que ningún operario humano podría hacer. La máquina nunca se cansa ni pierde concentración, y cada vez que se ejecuta el programa, descubre patrones de corte sorprendentes por su eficiencia.

4. Resultados y beneficios reales

Nuestro sistema ha sido probado exhaustivamente con datos reales proporcionados por Saint-Gobain, uno de los líderes mundiales en la fabricación de vidrio, comparándolo con los mejores métodos disponibles actualmente. Los resultados fueron los siguientes:

• Mejora del 4.3% en eficiencia de corte cuando se ejecuta durante 3 minutos
• Mejora del 3.3% con tiempos de cálculo más extensos (1 hora)

Estos resultados demuestran que puede ofrecer soluciones rápidas para decisiones inmediatas o soluciones más refinadas cuando se dispone de más tiempo para la planificación.

Traduciendo porcentajes en beneficios tangibles

Aunque estos porcentajes pueden parecer modestos a primera vista, sus implicaciones son extraordinarias cuando se trasladan a la escala industrial:

• Beneficio económico directo: Para una planta que procesa 50 toneladas diarias de vidrio, una mejora del 4 % representa un ahorro anual muy importante.
• Reducción de costos operativos: Menos material utilizado implica también menos manipulación, almacenamiento, transporte y gestión de residuos, lo que puede suponer un ahorro adicional de entre el 10 % y el 15 % sobre el ahorro directo en material.
• Impacto ambiental: La fabricación de cada tonelada de vidrio genera alrededor de 0.6 toneladas de CO₂, por lo que el ahorro anual significaría reducir las emisiones.
• Competitividad industrial: Estos ahorros permiten a las empresas ofrecer precios más competitivos, mejorar sus márgenes y destinar recursos a investigación y desarrollo de nuevos productos.

En un contexto internacional de creciente competencia y mayores exigencias ambientales, la optimización de procesos se ha convertido en una prioridad estratégica. Las empresas que no adopten estas tecnologías simplemente no podrán competir en el medio plazo.

5. Aplicaciones en otros sectores: cuando las matemáticas cruzan fronteras

El enfoque desarrollado para la industria del vidrio tiene potencial para transformar otros sectores que enfrentan desafíos similares de optimización de corte y aprovechamiento de materiales y espacios:

Industria de la madera

Los fabricantes de muebles enfrentan diariamente decisiones sobre cómo cortar tablones y láminas para maximizar el aprovechamiento. Los nudos y defectos de la madera representan un desafío similar a los defectos en el vidrio.

Industria metalúrgica

El corte de chapas metálicas para automoción, construcción o maquinaria sigue patrones que podrían optimizarse con adaptaciones de este enfoque, considerando las particularidades de cada material.

Logística y transporte

Nuestro enfoque puede adaptarse para optimizar la carga de contenedores y camiones. El reto es similar pero inverso: en lugar de cortar un material grande en piezas pequeñas, se busca acomodar eficientemente objetos pequeños en un espacio grande.

Las aplicaciones incluyen:

• Optimización de carga en camiones: Determinar la disposición óptima de cajas, palés y mercancías de diferentes tamaños para maximizar el espacio utilizado en cada camión. Considerando además restricciones como el peso máximo por eje, la distribución equilibrada de la carga y la accesibilidad para la descarga.
• Secuenciación integrada de rutas y carga: No solo optimizar cómo cargar un camión, sino también qué productos transportar en cada viaje y en qué orden realizar las entregas. Esta visión integrada permite resolver simultáneamente dos problemas tradicionalmente tratados por separado: qué llevar (problema de empaquetamiento) y en qué orden entregarlo (problema de ruta). 

6. Conclusiones: matemáticas que transforman la industria

Este estudio muestra cómo las Matemáticas junto con la Informática pueden transformar procesos industriales tradicionales, generando beneficios tangibles en eficiencia, economía y sostenibilidad.

A veces se cuestiona la aplicabilidad práctica de la investigación académica. Este proyecto es un ejemplo perfecto de cómo el conocimiento teórico, cuando se aplica a problemas reales en colaboración con la industria, puede generar soluciones innovadoras con impacto inmediato.

En un mundo donde los recursos son cada vez más escasos y la sostenibilidad es una prioridad, estas innovaciones representan un puente necesario entre la investigación académica y las necesidades industriales reales, demostrando que las matemáticas pueden ser, literalmente, una herramienta para construir un futuro más eficiente y sostenible.

La relevancia e impacto de este trabajo ha sido reconocida con el Premio Fundación BBVA a la Difusión del Conocimiento, otorgado a sus autores Francisco Parreño Torres, María Teresa Alonso Martínez y Ramón Álvarez-Valdés Olaguibel. Este galardón destaca la importancia de traducir la investigación matemática en soluciones prácticas para la industria.

Glosario

• Vidrio plano: Tipo de vidrio fabricado en forma de láminas continuas mediante el proceso de flotación sobre estaño fundido, utilizado principalmente en construcción y automoción.
• Optimización de corte: Campo de las matemáticas y la informática dedicado a minimizar el desperdicio al cortar materiales para obtener piezas de tamaños específicos.
• Patrón de corte: Diagrama que especifica la secuencia y posición exacta de cada corte para obtener un conjunto de piezas de una lámina.
• Corte de guillotina: Corte recto que atraviesa completamente una pieza rectangular, dividiéndola en dos rectángulos, similar al funcionamiento de una guillotina.
• Algoritmo aleatorizado: Método que introduce cierto grado de aleatorización en las decisiones para explorar un mayor rango de posibles soluciones y evitar estancarse en soluciones subóptimas.
• Búsqueda en haz: Técnica de optimización que explora múltiples soluciones parciales simultáneamente y selecciona las más prometedoras para continuar desarrollándolas, balanceando exploración y explotación.
• Metaheurística: Estrategia de optimización de alto nivel que combina diferentes técnicas para explorar eficientemente el espacio de soluciones posibles.

Cortesía de Muy Interesante

Dejanos un comentario: