Así fue la ingeniosa demostración que Leonardo da Vinci hizo del teorema de Pitágoras

Cuando pensamos en Leonardo da Vinci, solemos imaginar al pintor de la Mona Lisa o al inventor visionario, pero Leonardo también se adentró en el maravailloso mundo de las matemáticas. Uno de sus aportes menos conocidos es una elegante demostración del teorema de Pitágoras, la célebre relación a²+b²=c² entre los lados de un triángulo rectángulo. En este artículo exploraremos cómo concibió Leonardo su propia prueba de este teorema y qué nos revela sobre su manera de pensar en la confluencia de arte, ciencia y geometría.

La relación pitagórica (que dice que el área del cuadrado sobre la hipotenusa equivale a la suma de las áreas de los cuadrados sobre los catetos) se conocía desde la antigüedad, pero recibió el nombre de teorema de Pitágoras porque se cree que fue el filósofo griego Pitágoras quien aportó la primera demostración formal en el siglo VI a.C.. A lo largo de la historia han surgido decenas de demostraciones distintas —desde las recopiladas por Euclides hasta ingeniosas construcciones modernas—, pero pocas son tan originales y accesibles como la que ideó Leonardo da Vinci en pleno Renacimiento.

Un artista fascinado por las matemáticas

La imagen típica de Leonardo es la del maestro pintor e ingeniero, pero tras esa faceta artística había también una mente profundamente atraída por la matemática. Aunque nunca recibió educación formal en matemáticas y jamás llegó a dominar el álgebra, Leonardo poseía una notable intuición geométrica y habilidad espacial, cualidades presentes en muchos de sus proyectos e inventos. Para él, conceptos como la proporción, la simetría y la perspectiva eran clave para comprender la belleza de la naturaleza y las leyes del universo. De hecho, Leonardo llegó a describir la aritmética y la geometría como la “belleza de las obras de la naturaleza y ornato del mundo”, dejando claro el valor que otorgaba a las matemáticas para descifrar la realidad.

La obsesión de Leonardo por el rigor numérico quedó plasmada en sus propios escritos. En sus cuadernos afirmó que “no existe ninguna certeza cuando no se pueda aplicar alguna de las ciencias matemáticas”, subrayando que las ciencias solo eran verdaderas si se fundamentaban en demostraciones matemáticas. Fiel a esta filosofía, estudió con ahínco las obras clásicas de geometría. Hacia 1496, durante su estancia en Milán, entabló amistad con el fraile matemático Luca Pacioli, quien lo guio en el estudio de Euclides y con quien colaboró en tratados como De divina proportione (1509), un célebre compendio sobre la sección áurea que Leonardo ilustró con meticulosos dibujos de poliedros. Gracias a Pacioli, Leonardo profundizó más formalmente en la geometría (llegando incluso a ayudar en una edición de Los Elementos de Euclides), pero siempre la abordó desde una óptica visual y práctica, acorde con su formación autodidacta.

Una prueba visual e ingeniosa

La demostración pitagórica de Leonardo da Vinci aprovecha al máximo el razonamiento geométrico. Su planteamiento es sumamente gráfico: Leonardo dibujó un triángulo rectángulo con los tradicionales cuadrados adosados a cada lado y luego añadió elementos a la figura para reorganizar las áreas de manera reveladora. El resultado fue una argumentación visual tan clara que se ha dicho que “casi no necesita explicación” al contemplarla.

En su construcción, Leonardo agregó dos copias del triángulo inicial a la figura (el ECF y el HIJ en la imagen de abajo), colocándolas junto a los cuadrados ya dibujados. De este modo formó dos polígonos compuestos de igual superficie: uno incluye el cuadrado de la hipotenusa junto con dos triángulos, y el otro reúne los dos cuadrados de los catetos más dos triángulos. Si ambas figuras comparten el mismo área total, al retirar de cada una los dos triángulos añadidos (idénticos en ambas), las porciones restantes deben ser equivalentes. Esas porciones no son otras que el gran cuadrado construido sobre la hipotenusa en un caso, y la suma de los dos cuadrados menores construidos sobre los catetos en el otro. Así quedaba demostrado de forma puramente gráfica que c²=a²+b², confirmando el teorema de Pitágoras sin necesidad de fórmulas.

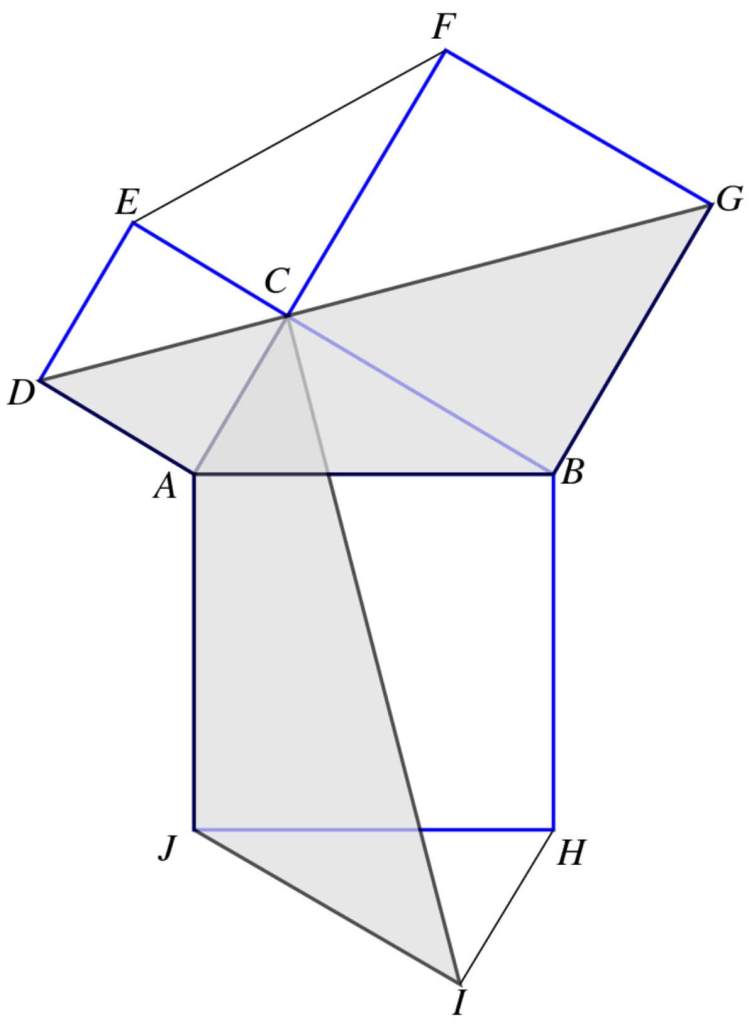
La genialidad de esta demostración reside en su simplicidad: más que cálculos, emplea comparaciones de forma y área. Leonardo había creado una suerte de rompecabezas geométrico que prueba el teorema de forma visual e intuitiva. Cabe destacar que esta preferencia por lo gráfico no es casual: al no estar versado en las técnicas algebraicas de su época, Leonardo confió en su poderosa percepción espacial para resolver el problema. Su prueba de Pitágoras es, en efecto, un ejemplo de “matemáticas sin palabras”, alineado con su talento de artista para comunicar ideas mediante imágenes.

Paso a paso

1. Se parte del triángulo rectángulo ABC, con los cuadrados construidos sobre sus lados.
2. Leonardo añade dos triángulos idénticos al original, llamados ECF y HIJ, que encajan en la figura sin alterar sus proporciones.
3. Con estas piezas forma dos polígonos compuestos:
   • El polígono ADEFGB, que incluye los dos cuadrados de los catetos.
   • El polígono ACBHIJ, que incluye el cuadrado de la hipotenusa.
4. Cada polígono puede dividirse en dos mitades simétricas, y Leonardo demuestra que esas mitades son equivalentes comparando lados y ángulos.
5. Para reforzar la equivalencia, muestra que un simple giro de la figura convierte una mitad en la otra, garantizando que son congruentes.
6. De esa manera concluye que los dos polígonos completos tienen la misma área total.
7. Finalmente, si a cada polígono se le quitan los triángulos añadidos (que son iguales), lo que queda es:
   • En un caso, los dos cuadrados de los catetos.
   • En el otro, el cuadrado de la hipotenusa.
8. El resultado es la igualdad buscada: la suma de las áreas de los catetos equivale al área de la hipotenusa.

No entiendo que al ser dos polígonos iguales se demuestre el teorema… ¡te lo explicamos!

1. El polígono ADEFGB está formado por:
   • Los dos cuadrados de los catetos (el de AB y el de AC).
   • Más dos copias del triángulo inicial (los que Leonardo añadió).
2. El polígono ACBHIJ está formado por:
   • El cuadrado de la hipotenusa (el de BC).
   • Más esas mismas dos copias del triángulo inicial.
3. Leonardo demuestra que los dos polígonos enteros tienen la misma área total.
4. Como ambos incluyen las mismas dos copias del triángulo, si quitamos esos triángulos de cada polígono lo que queda debe seguir siendo igual.
5. ¿Y qué queda?
   • En el polígono ADEFGB, al quitar los triángulos, solo quedan los dos cuadrados de los catetos.
   • En el polígono ACBHIJ, al quitar los triángulos, solo queda el cuadrado de la hipotenusa.
6. Por lo tanto, queda demostrado que la suma de las áreas de los cuadrados de los catetos equivale al área del cuadrado de la hipotenusa, que es exactamente el teorema de Pitágoras.

Arte, ciencia y legado renacentista

La demostración pitagórica de Leonardo ilustra a la perfección la unión entre arte y ciencia propia del Renacimiento. Un mismo hombre podía pintar una obra maestra y, a la vez, razonar sobre principios geométricos. Leonardo concebía la pintura como una ciencia, que debía apoyarse en principios matemáticos al igual que la óptica o la mecánica. Su interés por el teorema de Pitágoras no fue un capricho aislado, sino parte de un empeño mayor por encontrar armonía y orden numérico en el mundo. En su famoso dibujo del Hombre de Vitruvio, por ejemplo, explora las proporciones ideales del cuerpo humano mediante figuras y medidas geométricas, reflejando la convicción renacentista de que el universo está regido por patrones matemáticos.

Aunque la demostración de Leonardo no se publicó en su época en ningún tratado matemático, hoy la recordamos como una curiosidad histórica que reúne pedagogía y arte. Su valor reside, más que en aportar un avance técnico, en ejemplificar la brillantez multidisciplinar de Leonardo. Nos muestra cómo un artista e inventor podía también incursionar en la geometría teórica, guiado por la misma pasión de descubrir las verdades de la naturaleza. En última instancia, esta ingeniosa prueba visual refuerza la imagen de Leonardo da Vinci como el arquetipo del genio renacentista: un espíritu universal capaz de ver la profunda interconexión entre los números, las formas y la realidad.

Cortesía de Muy Interesante

Dejanos un comentario: