A veces, lo que parece un resultado vacío puede esconder algo profundo. Sumar una lista interminable de ceros suena como el camino más directo hacia la nada, pero en física cuántica, las apariencias engañan. Esta idea, en principio absurda, ha servido de clave para revelar comportamientos ocultos en ciertos materiales exóticos, donde las leyes clásicas de la física dejan de aplicarse. Si tu incredulidad no te permite aceptarlo, sigue leyendo.
Un nuevo estudio publicado en Physical Review X plantea que, en contextos fuera del equilibrio, una técnica matemática aparentemente trivial —la suma de ceros— puede tener consecuencias físicas reales. Lo han demostrado los investigadores Lucila Peralta Gavensky, Nathan Goldman y Gonzalo Usaj, al extender una fórmula clásica de la física de materiales a un terreno cuántico aún poco explorado. El hallazgo no solo resuelve una paradoja conceptual, sino que abre una vía para entender mejor cómo se comporta la materia cuando es impulsada por campos externos en condiciones no convencionales.
Una suma infinita que no da cero
En sistemas cuánticos impulsados periódicamente —llamados sistemas de Floquet— la energía no se conserva de la manera habitual. Esto los convierte en escenarios especialmente ricos para explorar nuevos estados de la materia. Lo curioso es que, al aplicar un campo magnético en estos sistemas, el resultado que deberían obtener los físicos parece insignificante: cada contribución individual se anula. Como si todos los caminos condujeran a cero.
Sin embargo, al aplicar una herramienta matemática conocida como sumación de Cesàro, los investigadores descubrieron que la suma total de esas contribuciones “nulas” da lugar a un resultado finito, cuantizado y físicamente significativo. Esta técnica, usada en matemáticas para asignar valor a series infinitas que no convergen, permitió a los autores interpretar correctamente una respuesta magnética que parecía invisible.
Lo interesante es que ese resultado final no solo tiene sentido matemático, sino que corresponde a una magnetización del sistema, un fenómeno físico medible. Es decir, lo que parecía una suma vacía escondía una propiedad cuántica topológica. Como se explica en el estudio, la respuesta obtenida a través de la sumación de Cesàro “corresponde a una magnetización en el volumen, cuantizada, que refleja un flujo de cuasienergía a lo largo del borde”.
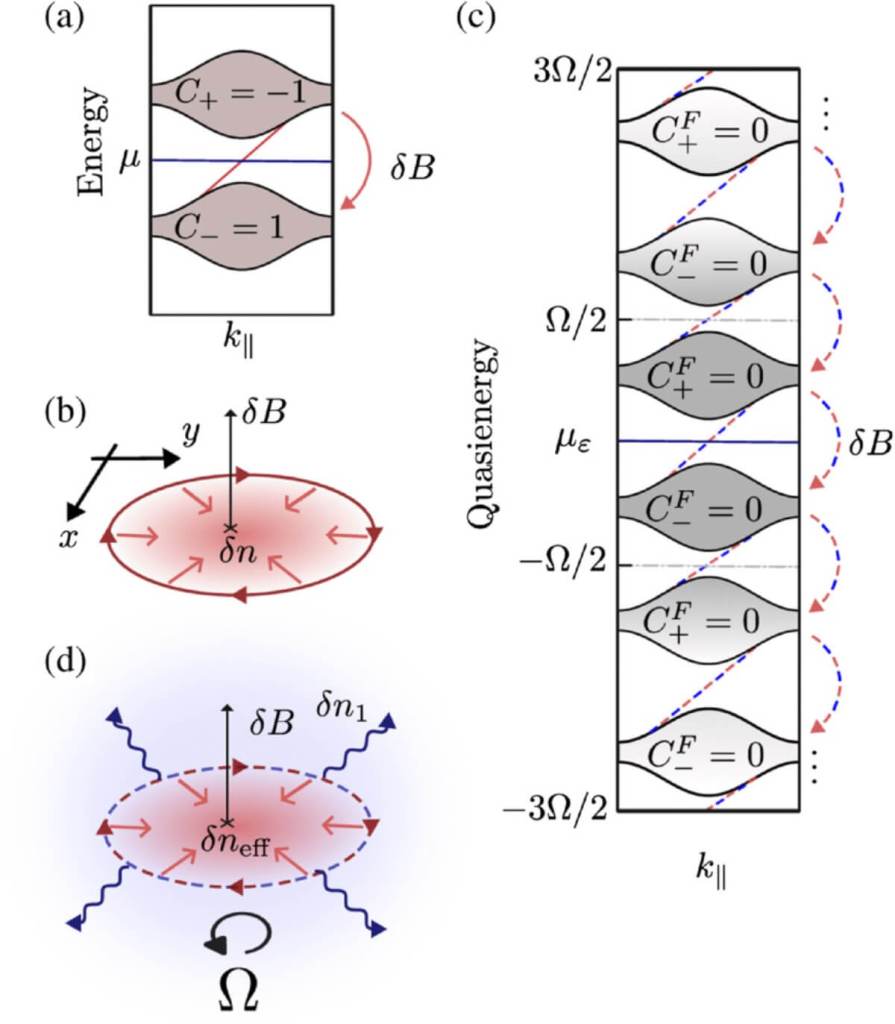
F
F, revelando tres regímenes distintos (I, II y III). En el recuadro inferior se representa el flujo de cuasienergía en los bordes del sistema, donde se origina la magnetización topológica. Todo el conjunto ilustra cómo una suma aparentemente nula de contribuciones da lugar a un efecto físico real y cuantificado. Fuente: Physical Review X
Un símil para entender que la suma de ceros da algo distinto de cero
En los sistemas cuánticos estudiados, cada nivel de energía individual —lo que los físicos llaman “modo de Floquet”— parece no contribuir al magnetismo cuando se analiza de forma aislada. Es decir, cada término da cero si se calcula su respuesta al campo magnético. Pero cuando se consideran todos los modos a la vez, de forma global y ordenada, aparece un resultado físico real. El truco no es sumar ceros como si fueran números normales, sino interpretar correctamente el comportamiento del conjunto completo con una técnica matemática válida: la sumación de Cesàro.
Una comparación simple: si uno ve una película cuadro por cuadro, cada imagen parece estática. Pero cuando se reproducen todas juntas, en orden, aparece el movimiento. Aquí ocurre algo parecido: aunque cada “cuadro” individual del sistema da cero, la secuencia entera revela un patrón. Ese patrón no es visible en los elementos por separado, pero sí aparece al analizarlos como un todo. El resultado es una magnetización cuantizada, real y medible, que no estaba en ningún punto aislado, sino en la estructura completa del sistema.

Topología cuántica en acción
La palabra “topología” se ha vuelto familiar gracias a materiales como los aislantes topológicos. En física, esta rama describe propiedades que no cambian aunque se deforme el sistema, como sucede con un dónut y una taza, que comparten una característica topológica: ambos tienen un agujero. En materiales cuánticos, la topología está relacionada con cómo se comportan los bordes del material en relación con su interior.
En condiciones de equilibrio, esta relación queda descrita por la llamada fórmula de Středa, que conecta el número de modos de borde protegidos con la respuesta magnética del sistema. Pero los sistemas de Floquet, que están fuera del equilibrio, exigían una nueva herramienta para hacer ese mismo tipo de conexión.
Lo que lograron los autores del estudio fue extender esta fórmula clásica al ámbito dinámico, creando una versión de la fórmula de Středa para sistemas impulsados periódicamente. Esto les permitió establecer una nueva conexión entre topología y magnetismo en un régimen antes inaccesible. Según el artículo, “este replanteamiento no solo resuelve una paradoja conceptual, sino que también ofrece una hoja de ruta para experimentos futuros”.
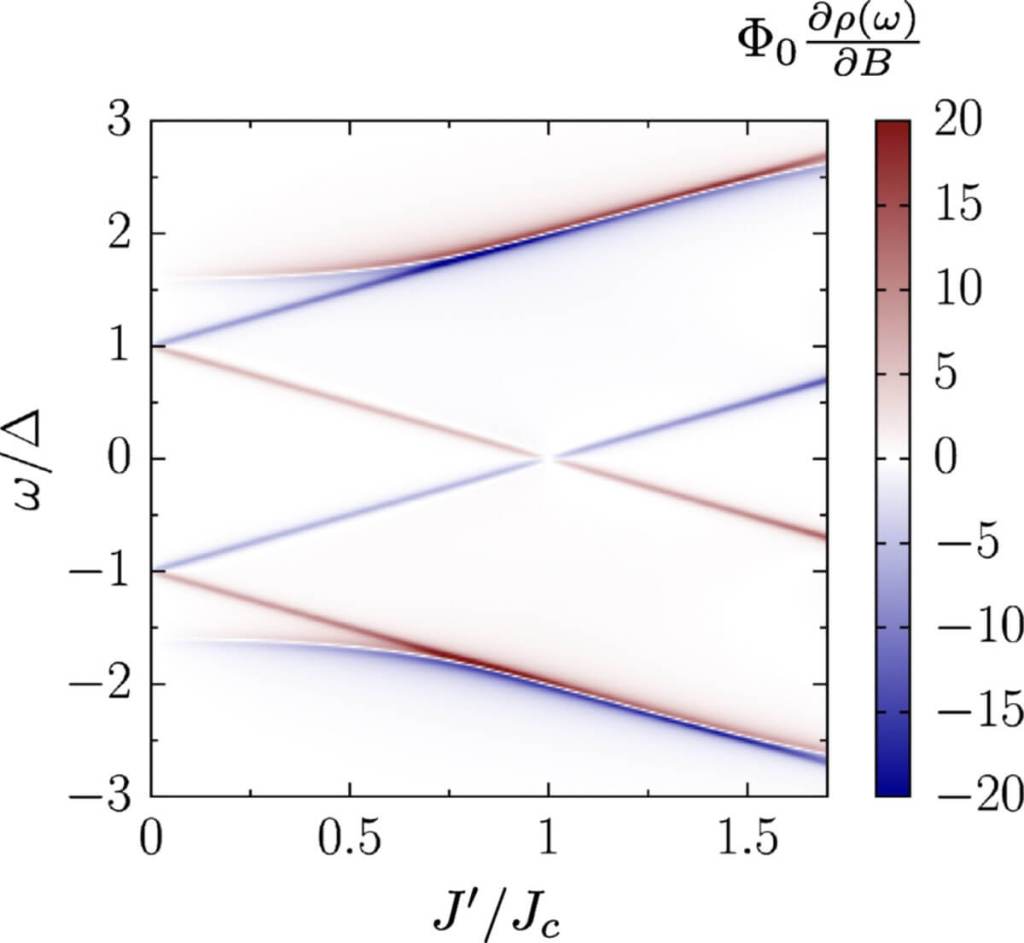
De lo abstracto a lo observable
Uno de los mayores logros del trabajo es que las ideas abstractas que propone no se quedan en el papel. Los investigadores delinean cómo este fenómeno podría observarse en la práctica, incluso en sistemas cuánticos desordenados. La clave está en medir la densidad de partículas en presencia de un campo magnético, lo que permitiría detectar la respuesta magnética obtenida mediante la sumación de Cesàro.
Además, se identificó un fenómeno adicional inesperado: un intercambio constante de energía entre el sistema y su entorno, inducido por el campo magnético. Esta especie de “bomba de energía” representa una firma distintiva de los sistemas de Floquet, que no puede observarse en materiales convencionales. En este sentido, el estudio abre la puerta a investigar posibles conexiones con materia cuántica en cavidades, donde incluso el campo de conducción es un objeto cuántico.
Este enfoque tiene el potencial de influir en el diseño de nuevas plataformas experimentales para estudiar fases exóticas de la materia, así como el desarrollo de dispositivos que funcionen bajo condiciones dinámicas extremas, donde los conceptos clásicos ya no bastan.
Un truco matemático con consecuencias físicas
La verdadera sorpresa del artículo reside en cómo una herramienta matemática, empleada desde hace tiempo en contextos puramente teóricos, se convierte en la clave para entender un fenómeno físico real. La sumación de Cesàro no es una invención nueva, pero su aplicación a este problema específico en física de materiales representa un avance conceptual.
El trabajo demuestra que incluso los modelos más abstractos pueden arrojar resultados tangibles cuando se aplican con rigor. En palabras del propio artículo: “Lo que parece nada —una suma de ceros— se convierte en algo profundo”. Esta frase resume bien el espíritu de la investigación, que desafía intuiciones comunes y muestra cómo la física teórica sigue teniendo un papel esencial en la exploración de nuevas realidades físicas.
Este resultado no solo tiene relevancia académica, sino que propone una nueva perspectiva para explorar estados cuánticos aún no clasificados, abriendo un camino hacia la comprensión de fases fuera del equilibrio y su posible utilidad tecnológica en el futuro.
Referencias
- Lucila Peralta Gavensky, Nathan Goldman y Gonzalo Usaj, Středa Formula for Floquet Systems: Topological Invariants and Quantized Anomalies from Cesàro Summation, Physical Review X (2025). DOI: 10.1103/b3pw-my97.
Cortesía de Muy Interesante
Dejanos un comentario: