Fuente de la imagen, Getty Images
-
- Autor, Kit Yates
- Título del autor, BBC Future*
Solo les tomó ocho minutos. En esos 480 segundos, los ladrones ascendieron por una plataforma mecánica hasta un balcón del primer piso del museo del Louvre en París, donde cortaron una ventana a plena luz del día.
Una vez dentro, rompieron dos vitrinas y escaparon con ocho joyas de la corona de la época napoleónica, de un valor incalculable. Fue un robo audaz que ha conmocionado profundamente a Francia.
Siete sospechosos han sido arrestados por el robo. Sin embargo, una de las preguntas que persiste en la investigación es por qué los ladrones no fueron descubiertos antes.
En una audiencia ante el Senado francés inmediatamente después del robo, Laurence des Cars, directora de la institución de fama mundial, admitió que el museo había fallado en la protección de las joyas de la Corona.
Reconoció que la única cámara que cubría el balcón utilizado por los ladrones estaba mal orientada y un informe preliminar reveló que una de cada tres salas del ala Denon, donde se produjo el robo, carecía de cámaras de seguridad.
En términos más generales, Des Cars reconoció que los recortes en vigilancia y personal de seguridad habían dejado al museo vulnerable e insistió en que el sistema de seguridad del Louvre debía reforzarse para abarcar todos los rincones.
Según el Ministerio de Cultura francés, las alarmas del museo sonaron correctamente. Sin embargo, este es el tercer robo de gran repercusión en museos franceses en dos meses, lo que ha llevado al ministerio a implementar nuevos planes de seguridad en todo el país.
Si bien no cabe duda de que la seguridad en los museos modernos es un asunto complejo y costoso, existe un intrigante problema matemático de hace 50 años que aborda precisamente esta cuestión.
La pregunta es: ¿cuál es el número mínimo de guardias —o, equivalentemente, de cámaras de videovigilancia de 360 grados— necesario para mantener un museo completo bajo vigilancia? Se conoce como el problema del museo o el problema de la galería de arte.
La solución es elegante.

Fuente de la imagen, Getty Images
Geometría, al rescate
Supondremos que todas las paredes de nuestro museo imaginario son rectas, de modo que la planta sea lo que los matemáticos llaman un polígono, una figura con aristas y esquinas definidas.
Las cámaras deben estar en posiciones fijas, pero con visión en todas direcciones. Para asegurar que todo el museo esté cubierto, debemos poder trazar una línea recta desde cualquier punto de la planta hasta al menos una de las cámaras.
Tomemos como ejemplo la galería hexagonal de la izquierda en el diagrama inferior.
Independientemente de dónde coloquemos la cámara, podremos ver el suelo y las paredes de todo el espacio. Cuando se puede ver desde cualquier posición cualquier otra, decimos que la galería tiene forma de polígono convexo.
La galería en forma de L del centro no es convexa, lo que significa que la colocación de las cámaras es limitada, pero aún podemos encontrar puntos desde donde una sola cámara puede abarcar toda la galería.
Una galería en forma de Z necesita dos cámaras para cubrirla; siempre hay zonas que una sola cámara no alcanza a cubrir.
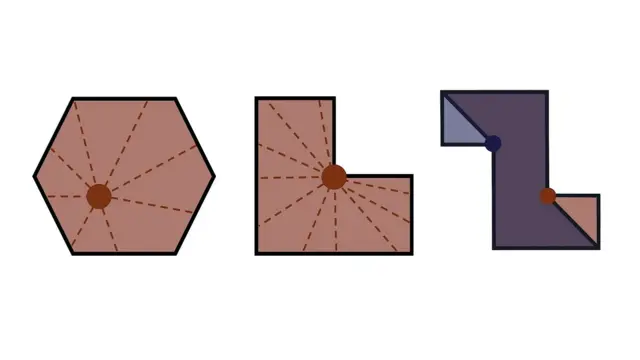
Fuente de la imagen, Kit Yates
Para planos más interesantes (como el inusual plano de 15 lados que se muestra a continuación), resulta mucho más difícil determinar cuántas cámaras se necesitarán o dónde colocarlas.
Afortunadamente para los directores de museos con presupuestos ajustados, el teórico de grafos Václav Chvátal resolvió el problema de los museos en términos generales poco después de que se planteara en 1973.
La respuesta, resulta, depende del número de esquinas (o, como las llaman los matemáticos, “vértices”), ya que habrá tantas paredes como esquinas en una sala. Una simple división nos ayuda a calcular cuántas cámaras se necesitan.
Al dividir el número de esquinas de una sala entre tres, sabremos cuántas cámaras se necesitan para cubrirla, suponiendo que tengan un campo de visión completo de 360 grados.
Esto funciona incluso para formas complejas como nuestra peculiar galería de 15 lados que se muestra a continuación. En este caso, hay 15 esquinas, por lo que 15 dividido entre tres es igual a cinco.

Fuente de la imagen, Kit Yates
Esto funciona incluso si el número de esquinas no es divisible exactamente por tres. Para una galería de 20 lados, por ejemplo, la respuesta es seis y dos tercios. En estos casos, se puede usar el número entero, por lo que nunca necesitaríamos más de seis cámaras en una sala de 20 lados.
Triangulando la solución
En 1978, Steve Fisk, profesor de matemáticas en el Bowdoin College de Maine, en EE. UU., ideó una demostración —considerada una de las más elegantes de todas las matemáticas— de este límite inferior en el número de cámaras necesarias.
Su estrategia consistía en dividir la galería en triángulos (véase la imagen de la izquierda en la figura inferior).
Luego demostró que se pueden elegir solo tres colores —por ejemplo, rojo, amarillo y azul— y asignar un color diferente a las esquinas de cada triángulo. Esto significaría que cada triángulo de la galería tendría un color diferente en sus tres esquinas (véase la imagen de la derecha en la figura inferior para un ejemplo).
Esto se conoce como “tricolorear” las esquinas.
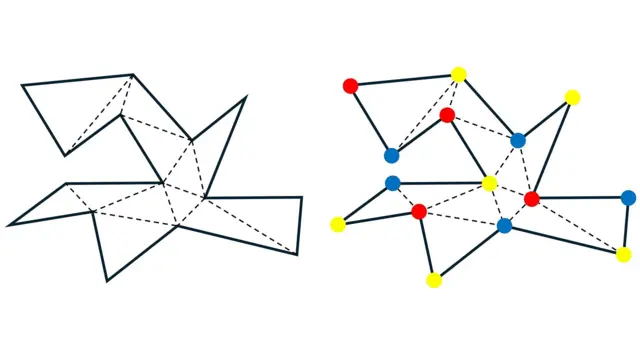
Fuente de la imagen, Kit Yates
Los triángulos son uno de esos polígonos convexos que mencionamos antes, así que una cámara colocada en cualquier vértice (o en cualquier punto del triángulo) puede ver todos sus puntos.
Cada triángulo tiene vértices de cada uno de los tres colores. Esto significa que puedes elegir solo un color y colocar cámaras en esas posiciones. Dichas cámaras podrán ver cada parte de cada triángulo y, por lo tanto, cada parte de la galería.
Pero lo mejor está por venir.
La genialidad de la prueba de Fisk reside en que basta con elegir el color con la menor cantidad de puntos para cubrir toda la galería. En la figura de 15 lados mostrada arriba, al elegir los puntos rojos, podemos usar solo cuatro cámaras.
De hecho, el punto rojo en la esquina superior izquierda no es necesario, ya que la siguiente cámara roja puede cubrir todo su espacio de vigilancia.
Por lo tanto, incluso podríamos usar tres cámaras para esta galería. Esto es especialmente cierto si instalamos cámaras omnidireccionales modernas, en lugar de las antiguas cámaras de circuito cerrado de televisión de gran angular, que necesitarían abarcar un área extensa para brindar una cobertura completa, creando puntos ciegos temporales.
Sin embargo, conviene recordar que muchos museos tradicionales, como el Louvre, tienen salas mayormente rectangulares.
Afortunadamente, una variante del problema de las galerías de arte demuestra que cuando las paredes se unen en ángulo recto, solo se necesita una cámara para cubrir toda la sala.
Puntos ciegos

Fuente de la imagen, Getty Images
En su testimonio, Des Cars también reconoció que las cámaras perimetrales del Louvre no cubren todas las paredes exteriores.
“No detectamos la llegada de los ladrones con la suficiente antelación… conocemos la debilidad de nuestra seguridad perimetral”, afirmó.
Afortunadamente, existen versiones del problema, conocidas como “el problema de la fortaleza” o “el problema de la prisión”, que también solucionan el problema de la cobertura de las cámaras en el exterior de un edificio.
Sin embargo, lo que ambas variantes revelan es que encontrar los puntos de observación adecuados es esencial.
Pero es importante reconocer que los ladrones que entran por las galerías públicas no son la única amenaza a la que se enfrentan los museos.
El Museo Británico de Londres, por ejemplo, vio desaparecer en 2011 un anillo de Cartier valorado en US$950.000 de una colección que no estaba expuesta al público. Joyas del museo aparecieron a la venta en eBay en 2020, supuestamente sustraídas por uno de los propios conservadores del museo.
Además de los robos, los museos también deben proteger sus colecciones del vandalismo, los incendios y otras formas de destrucción.
Aun así, el problema de las galerías de arte merece la atención de quienes están fuera de los venerados recintos de los museos. Tiene aplicaciones en diversos campos donde la visibilidad y la cobertura son cruciales.
En robótica, por ejemplo, ayuda a los sistemas autónomos a mejorar su eficiencia y prevenir colisiones. En planificación urbana, sirve de base para la ubicación de antenas de radio, estaciones de transmisión de telefonía móvil o detectores de contaminación para garantizar una cobertura completa de los espacios públicos.
Las estrategias de gestión de desastres utilizan principios similares para posicionar drones y realizar reconocimientos aéreos de grandes catástrofes o para ubicar puestos médicos de campaña.
En edición de imágenes y visión artificial, el problema de la galería de arte puede ayudar a identificar las regiones visibles dentro de una escena.
Puede contribuir a garantizar que los artistas estén siempre bien iluminados en el escenario e incluso ayudar a los museos a asegurar que sus galerías cuenten con la iluminación adecuada.
El Louvre no respondió a las preguntas de la BBC sobre si conocía las soluciones que ofrece el problema del museo; sin duda, tiene asuntos más urgentes que atender.
Pero ahora que museos y galerías de arte de todo el mundo revisan su seguridad tras el robo del Louvre, no está de más recordar las lecciones que ofrece este problema matemático de hace 50 años.
Esta es una adaptación al español de una historia que se publicó en inglés en BBC Future. Si quieres acceder a la versión original, haz clic aquí.

Suscríbete aquí a nuestro nuevo newsletter para recibir cada viernes una selección de nuestro mejor contenido de la semana.
Y recuerda que puedes recibir notificaciones en nuestra app. Descarga la última versión y actívalas.
Cortesía de BBC Noticias
Dejanos un comentario: