En 1928, un joven físico soviético llamado George Gamow publicó un artículo que, con el tiempo, se convertiría en uno de los pilares de la física nuclear moderna. Su título, Zur Quantentheorie des Atomkernes (“Sobre la teoría cuántica del núcleo atómico”), puede parecer lejano para el público general. Pero lo que explicó en aquellas páginas va al corazón de una pregunta asombrosa: ¿por qué brillan las estrellas?
En el centro de ese trabajo hay una imagen discreta, casi esquemática, que pasa fácilmente desapercibida: una simple gráfica con una barrera de energía y una partícula intentando atravesarla. Esta figura —la Figura 2 del artículo— representa una idea revolucionaria que sacudió los cimientos de la física clásica: el efecto túnel cuántico. Y aunque parezca increíble, sin este fenómeno el Sol y todas las estrellas del universo no podrían producir energía ni luz.
Una barrera imposible… en la física clásica
Gamow partía de un problema que desconcertaba a los físicos de su tiempo: el de la emisión alfa. Algunos átomos pesados, como el uranio, expulsaban partículas alfa (núcleos de helio) a pesar de que, según la física clásica, no podían escapar del núcleo, pues la barrera de repulsión eléctrica era demasiado alta para su energía.
Tal como Gamow explica: “Para escapar, la partícula alfa tendría que superar una barrera de potencial de altura U0. Pero su energía, como se ha demostrado experimentalmente, es mucho menor que U0”.
Clásicamente, eso sería como si una pelota rodara cuesta arriba por una colina más alta que su impulso: simplemente no puede. Pero en el mundo cuántico, las reglas son otras.
La clave está en la Figura 2
La Figura 2 del artículo muestra una partícula enfrentando una barrera de energía. A la izquierda, se mueve libremente. Al llegar a la región central (la barrera), su energía es insuficiente. Pero en lugar de rebotar por completo, una parte de la onda asociada a la partícula logra atravesar y aparece al otro lado.
Es lo que hoy conocemos como efecto túnel cuántico. Como dice Gamow:
“En la mecánica ondulatoria, siempre existe una probabilidad distinta de cero de que una partícula pase de una región a otra de igual energía, incluso si están separadas por una barrera de potencial arbitrariamente alta pero finita”.
En otras palabras: lo improbable no es imposible.
Aplicación estelar: cómo comienza la fusión
Este fenómeno, inicialmente pensado para explicar la desintegración radiactiva, resultó ser clave en otro lugar mucho más grande: el núcleo del Sol. Allí, los protones quieren fusionarse y liberar energía. Pero tienen un problema: se repelen eléctricamente. Las temperaturas son enormes, sí, pero aún así no bastan para vencer esta repulsión si nos guiamos por la física clásica. Sin embargo, gracias al efecto túnel, algunos protones logran atravesar esta barrera y fusionarse, iniciando la cadena de reacciones que mantiene viva la estrella.
Sin túnel cuántico, la fusión en estrellas como el Sol simplemente no ocurriría. Y sin fusión, no habría luz, ni calor, ni elementos más pesados en el universo.
La fórmula que lo hizo cuantificable
Gamow no solo sugirió el túnel, también lo cuantificó. Usando la ecuación de Schrödinger, resolvió un modelo con una barrera rectangular de energía y halló cómo calcular la probabilidad de que una partícula atraviese esa barrera por efecto túnel. Esa probabilidad no es cero, pero disminuye de forma exponencial según las propiedades de la barrera y la energía de la partícula.
La expresión central que obtuvo (en forma simplificada) es:Donde:
- es el número de Euler (la base de los logaritmos naturales),
- es la constante de Planck reducida,
- es la masa de la partícula,
- es la altura de la barrera,
- es la energía de la partícula,
- es el grosor de la barrera.
Cuanto más alta o más ancha es la barrera, menor es la probabilidad de que la partícula la atraviese. Pero mientras esa barrera tenga una altura y un grosor finitos, la probabilidad nunca será cero.
Cómo entender qué dice esta fórmula
Puede que a primera vista esta fórmula parezca intimidante, pero en realidad dice algo muy sencillo: que la probabilidad de que una partícula atraviese una barrera disminuye rápidamente cuando la barrera es más gruesa, más alta, o cuando la partícula tiene menos energía.
Veamos qué representa cada parte:
- El símbolo e representa un número especial en matemáticas, como el famoso π (pi). Es la base de los logaritmos naturales y aparece cada vez que algo cambia muy rápido, como aquí.
- Lo que está en el exponente (arriba del ) es lo que controla cuánto se reduce esa probabilidad.
- l es el grosor de la barrera: cuanto más ancho el muro, más difícil cruzarlo.
- U0−E mide la diferencia entre la altura del muro y la energía de la partícula: si la partícula tiene poca energía, la diferencia es grande, y la fórmula nos dice que será muy poco probable que pase.
- Todo eso está dentro de una raíz cuadrada, y dividido por , la constante de Planck reducida, que es lo que convierte esta ecuación en una predicción puramente cuántica.
En resumen: Una partícula con poca energía, frente a una barrera alta y ancha, casi nunca pasará. Pero cuánticamente, siempre tiene una pequeña posibilidad. Y esa pequeña posibilidad es la que hace brillar a las estrellas.
De núcleos radiactivos al corazón del Sol
Gamow aplicó su teoría a datos reales de emisión alfa y obtuvo resultados notablemente cercanos a los valores medidos en laboratorio. Derivó una fórmula que explicaba la relación entre la energía de las partículas emitidas y la constante de desintegración, y encontró que coincidía con las mediciones conocidas hasta ese momento.
“La coincidencia en el orden de magnitud muestra que el supuesto fundamental de la teoría debe ser correcto”.
Esta fue una de las primeras conexiones firmes entre la física cuántica y los fenómenos nucleares reales.
Una gráfica modesta, una idea descomunal
En retrospectiva, resulta casi poético que una figura tan sencilla —una partícula ante una pared de energía— haya contenido una verdad tan profunda: el universo no es solo lo que vemos, sino también lo que puede ocurrir, aunque sea con muy baja probabilidad.
Gracias al efecto túnel descrito en 1928 por Gamow, sabemos hoy que las estrellas brillan no porque puedan vencer todas las barreras, sino porque la física cuántica permite atravesarlas.
Punto extra: la doble barrera y la danza cuántica de las partículas
Tras presentar el modelo simple de una sola barrera, Gamow fue un paso más allá en su artículo de 1928 con una figura más compleja y poderosa: la Figura 3. Allí propuso un sistema con dos barreras simétricas separadas por una región interna, representando de forma más precisa el interior de un núcleo atómico.
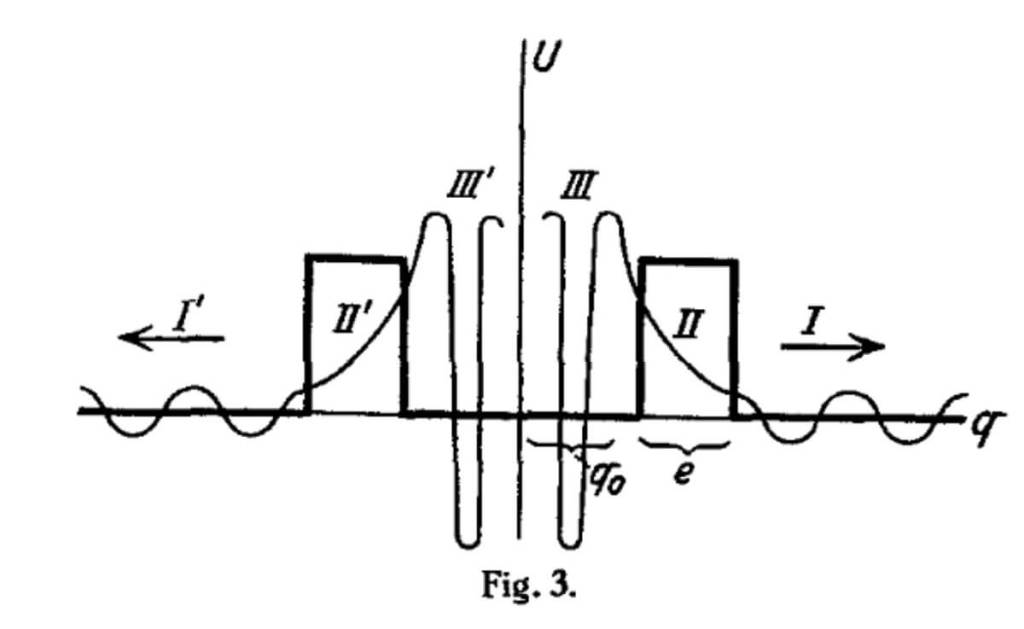
En esta figura, la partícula (como una alfa) no está simplemente frente a una pared, sino oscilando dentro del núcleo, atrapada entre dos potenciales de repulsión. La función de onda en el interior (región III) oscila como una onda estacionaria, mientras que decrece exponencialmente al atravesar las barreras (regiones II y II’), y reaparece con menor amplitud en el exterior (regiones I y I’).
Esta es la firma del efecto túnel con decaimiento:
“Si la energía total se permite ser compleja, con una parte imaginaria pequeña, la amplitud de la onda decrece con el tiempo”.
Este cambio refleja que el sistema pierde partículas en el tiempo —es decir, que el núcleo se desintegra lentamente, tal como se observa en la naturaleza. El uso de una energía compleja fue una innovación audaz: introdujo por primera vez en la física cuántica la idea de una vida media como propiedad derivada de la forma de la función de onda.
En esencia, esta figura no solo embellece el artículo: convierte la teoría en una explicación completa del fenómeno de la desintegración radiactiva, uniendo mecánica cuántica, estadística y observación experimental.
Referencias
- Gamow, G. (1928). Zur Quantentheorie des Atomkernes. Zeitschrift für Physik, 51, 204–212. https://doi.org/10.1007/BF01343196
Cortesía de Muy Interesante
Dejanos un comentario: