Los mosaicos no son solo decoraciones que embellecen paredes o pisos. Desde hace siglos, estas formas geométricas repetitivas han fascinado a artistas y matemáticos por igual. En la obra de M.C. Escher, por ejemplo, las teselaciones se transforman en peces, aves o manos que se dibujan entre sí. Pero más allá de su valor visual, existe una dimensión matemática de los mosaicos que está empezando a revelarse con nuevas herramientas teóricas. En particular, las teselaciones en geometría hiperbólica —un tipo de espacio que se curva hacia adentro como una silla de montar— están demostrando ser claves para resolver problemas complejos de análisis matemático y física.
Un nuevo estudio de Heinrich Begehr y Dajiang Wang publicado en la revista Applicable Analysis muestra cómo ciertas teselaciones permiten construir soluciones explícitas a problemas de frontera en análisis complejo, física matemática e ingeniería. El trabajo explora el uso del llamado principio de reflexión tipo mosaico, una técnica que permite extender funciones complejas por medio de simetrías geométricas. Lejos de ser solo un ejercicio visual, este enfoque ofrece herramientas potentes para resolver ecuaciones diferenciales parciales y entender estructuras subyacentes en contextos como la teoría cuántica o la ingeniería electromagnética.
Simetría que resuelve ecuaciones
La idea central del estudio es que las teselaciones pueden utilizarse como un andamiaje matemático para extender funciones en regiones complicadas del plano. Usando reflexiones repetidas a través de los bordes de ciertas figuras geométricas, los autores logran generar patrones altamente simétricos. Estas figuras actúan como “espejos” que permiten construir soluciones a problemas como los de Dirichlet o Neumann, clásicos en el campo de las ecuaciones diferenciales.
El procedimiento se basa en aplicar el principio de reflexión sucesiva dentro de polígonos circulares, cuyas fronteras están compuestas por arcos de circunferencia. Al reflejar la función a través de cada borde, se va cubriendo todo el plano con copias del dominio original, de forma similar a cómo se multiplican las imágenes en un espejo tridimensional. Esta técnica es especialmente útil para representar funciones armónicas, es decir, aquellas que satisfacen ciertas condiciones de equilibrio físico o potencial.
Según el artículo original: “La belleza en las matemáticas no es solo una noción estética, sino algo con profundidad estructural y eficiencia”. Esta afirmación resume el objetivo del trabajo: encontrar en la regularidad geométrica una forma de atacar problemas que, hasta ahora, requerían métodos más abstractos o numéricos.
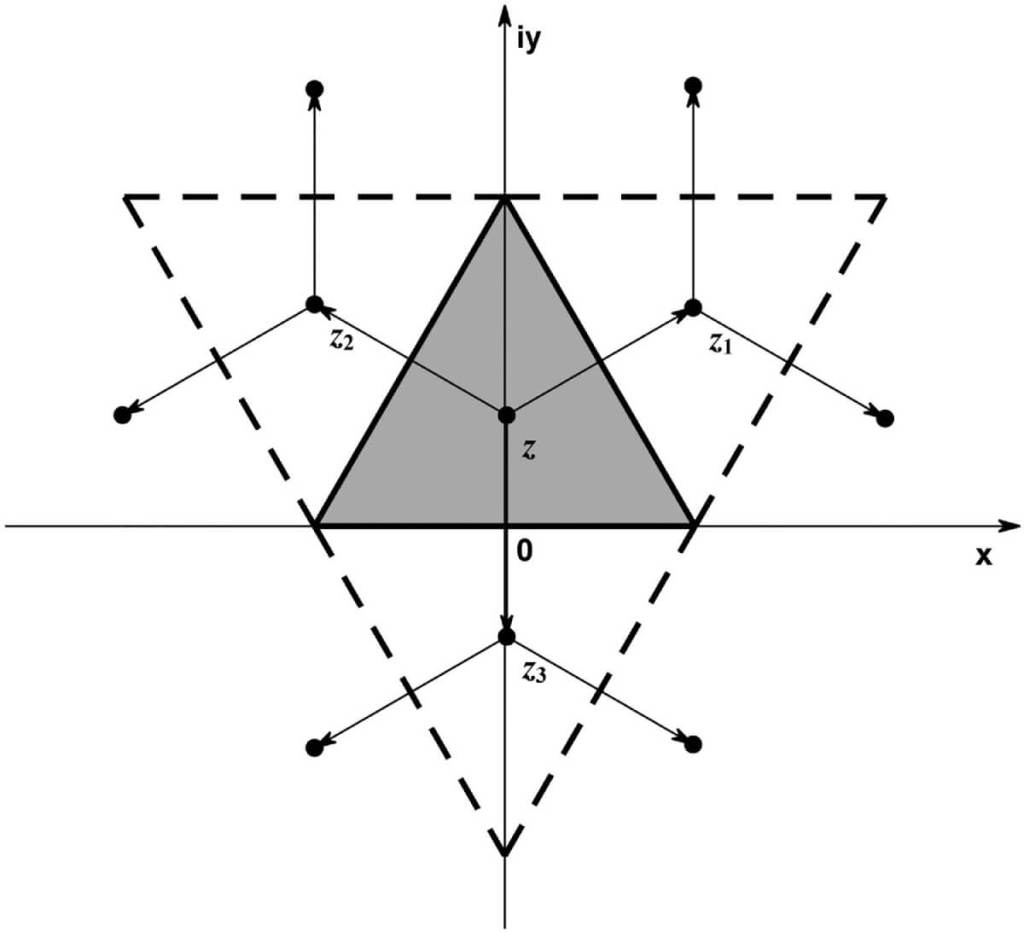
Funciones núcleo y su conexión con los mosaicos
Uno de los logros más importantes del enfoque propuesto es la construcción de fórmulas explícitas para ciertas funciones núcleo, herramientas matemáticas esenciales en la resolución de ecuaciones de frontera. En particular, los autores presentan resultados concretos para los núcleos de Green, de Neumann y de Schwarz, fundamentales en física y análisis complejo.
Estas funciones permiten representar soluciones de manera integral, es decir, como sumas continuas sobre los bordes de una región. Lo destacable aquí es que, gracias al uso del principio de reflexión tipo mosaico, es posible obtener expresiones exactas para estas funciones en dominios que, de otro modo, serían intratables. Según el paper, “estas representaciones integrales son de gran utilidad para resolver problemas en regiones con geometrías complejas” .
El método no se limita al plano euclidiano. De hecho, una de las contribuciones más interesantes es su extensión a la geometría hiperbólica, donde los mosaicos adoptan formas que desafían la intuición visual. En estos contextos, el uso de triángulos especiales —llamados triángulos de Schweikart— permite aplicar el mismo principio de reflexión y derivar resultados análogos.
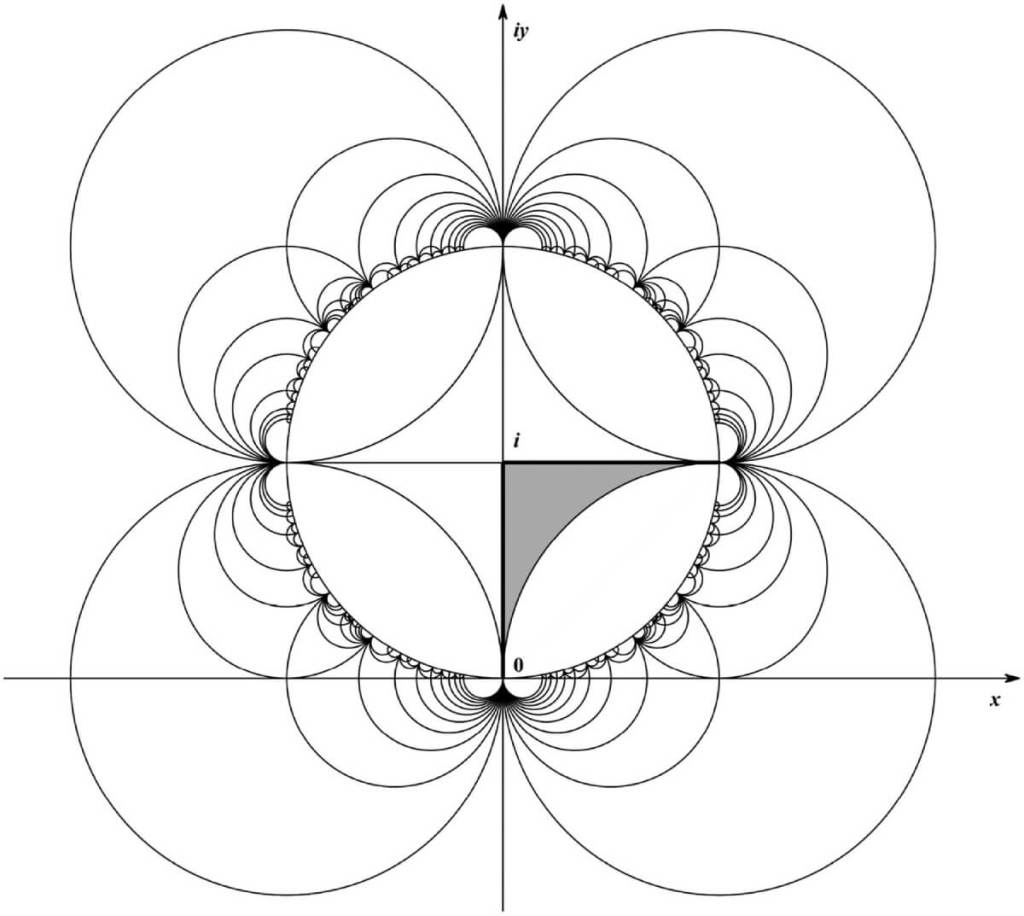
Los triángulos de Schweikart y la belleza hiperbólica
Los llamados triángulos de Schweikart son figuras con un ángulo recto y dos ángulos de valor cero. Estas estructuras solo existen en geometría hiperbólica, y permiten realizar un teselado completo del disco hiperbólico. En el contexto visual, producen patrones de gran simetría y atractivo, pero lo realmente importante es que sirven como base para extender el método de los mosaicos a espacios curvos.
En otro artículo técnico publicado por Heinrich Begehr en Complex Variables and Elliptic Equations, se muestra cómo construir la función de Green armónica para uno de estos triángulos, utilizando el mismo principio de reflexión. Esto demuestra que el método no solo es elegante, sino también versátil. En este espacio no euclidiano, las propiedades de simetría permiten formular soluciones exactas a problemas que aparecen, por ejemplo, en modelos de gravedad cuántica o óptica no lineal.
Además, este tipo de figuras despierta interés más allá de la matemática pura. Como señala Wang: “Esperamos que nuestros resultados no solo resuenen en matemáticas puras o física matemática, sino que también inspiren ideas en arquitectura o gráficos por computadora”.
Una tradición matemática con raíces en Berlín
El grupo de investigación de Begehr en la Freie Universität Berlin lleva cerca de dos décadas trabajando con lo que llaman los “mosaicos espejo de Berlín”. Inspirados en el principio de reflexión unificado de Hermann Amandus Schwarz, estos mosaicos consisten en reflejar polígonos circulares hasta llenar todo el plano. Más allá de su valor estético, este proceso permite construir representaciones explícitas de funciones complejas.
Curiosamente, el método tiene raíces visuales en técnicas antiguas. Según se cita en el artículo: “Los matemáticos solían utilizar espejos de tocador de tres caras para producir secuencias infinitas de imágenes”, comenta Begehr. Hoy en día, los programas informáticos permiten replicar esos patrones con precisión, y lo más importante: permiten extraer fórmulas exactas que facilitan la resolución de problemas complejos.
Esta línea de investigación ha dado lugar ya a múltiples tesis y trabajos de doctorado, no solo en Berlín, sino también en otras universidades internacionales. La combinación de visualización geométrica y rigor matemático está generando una comunidad creciente de investigadores interesados en el tema.
Más allá del arte: cuando lo visual se vuelve herramienta
Las teselaciones, tradicionalmente asociadas al arte islámico o al diseño gráfico, están demostrando ser mucho más que un recurso decorativo. En este nuevo contexto, se convierten en instrumentos analíticos, capaces de ofrecer soluciones elegantes a problemas reales. Este enfoque representa un cruce entre la estética visual y la lógica matemática, donde lo bello se vuelve útil.
El trabajo de Begehr y Wang abre nuevas posibilidades tanto en matemáticas puras como aplicadas. Su método puede emplearse en contextos tan variados como la ingeniería de materiales, la simulación física o incluso el diseño de algoritmos gráficos. Además, la claridad visual que ofrecen los mosaicos permite que conceptos abstractos sean representados de manera intuitiva, lo que facilita su uso en entornos educativos y tecnológicos.
Este diálogo entre simetría, geometría y análisis sugiere una nueva forma de hacer matemáticas: una que no teme apoyarse en la belleza como guía para el descubrimiento.
Referencias
Cortesía de Muy Interesante
Dejanos un comentario: