Del Big Bang a las leyes ocultas: la red neuronal que intenta explicar el universo con inteligencia artificial

Algunas de las ideas más poderosas de la ciencia han nacido no en grandes laboratorios, sino en libretas escolares, donde las ecuaciones se cruzaban con la intuición. Fue así como Andrei Kolmogorov y Vladimir Arnold formularon una teoría matemática que, décadas después, ha inspirado un nuevo modelo de inteligencia artificial capaz de hacer algo que los científicos llevan tiempo buscando: descubrir leyes de la naturaleza directamente desde los datos. Hoy, esa vieja intuición cobra vida en forma de una red neuronal que no solo aprende a predecir, sino que también ofrece explicaciones comprensibles para los humanos.

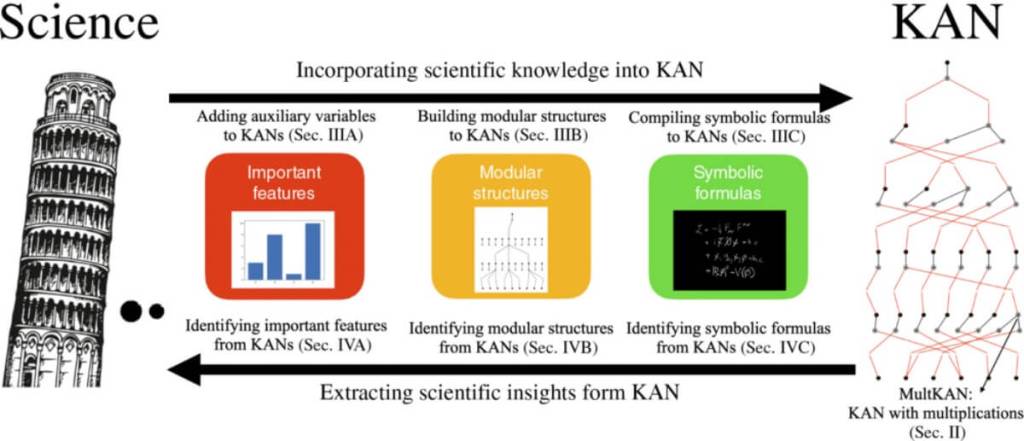
En un artículo publicado por un equipo internacional liderado por científicos del MIT, se presenta la arquitectura Kolmogorov–Arnold Networks (KANs), una nueva forma de red neuronal diseñada específicamente para facilitar el descubrimiento simbólico. A diferencia de las redes neuronales tradicionales, que suelen actuar como cajas negras, las KANs permiten interpretar los resultados de forma directa y simbólica. Este avance promete una transformación profunda en cómo se utilizan los modelos de inteligencia artificial en disciplinas como la física, la biología o la ingeniería.

Una red neuronal con sentido físico

Las redes neuronales tradicionales están diseñadas para predecir, pero no para explicar. Por su propia estructura, muchas veces resultan difíciles de interpretar. En cambio, las KANs están construidas para representar funciones de forma explícita, aprovechando una idea matemática conocida como teorema de Kolmogorov–Arnold. En lugar de usar pesos fijos y funciones de activación como en las redes convencionales, las KANs modifican directamente las funciones que aplican en cada nodo, permitiendo así un grado de flexibilidad mucho mayor.

Una de las ventajas clave de este enfoque es su capacidad para representar fórmulas de manera simbólica, lo que significa que no solo se puede saber qué predice la red, sino también cómo lo hace. Según los autores, “KANs presentan ventajas tanto en tareas de regresión como de descubrimiento simbólico”, lo cual permite utilizarlas para problemas donde la comprensión de la estructura matemática es tan importante como la precisión en la predicción.

Esto abre una puerta completamente nueva: la posibilidad de que una red neuronal no solo imite el conocimiento humano, sino que lo genere, extrayendo directamente de los datos leyes físicas o relaciones estructurales que antes requerían años de trabajo teórico.

Redescubriendo la física con IA

El equipo de investigación sometió a las KANs a pruebas exigentes: ¿podían estas redes descubrir, por sí solas, leyes conocidas de la física? Los resultados fueron sorprendentes. Por ejemplo, en uno de los experimentos, una KAN logró redescubrir la fórmula relativista de la masa en función de la velocidad, una relación fundamental en la teoría especial de la relatividad.

El artículo indica que “KANs no solo producen aproximaciones numéricas precisas, sino que extraen fórmulas cerradas en formato simbólico, como en el caso de la masa relativista”. Esta capacidad representa un avance notable respecto a otros modelos de inteligencia artificial, que solo pueden predecir resultados sin ofrecer una comprensión directa.

También se realizaron experimentos con sistemas dinámicos, donde las KANs identificaron cantidades conservadas(como la energía o el momento), lo cual es esencial para entender la evolución de un sistema físico. En estas tareas, el modelo mostró ser capaz de identificar simetrías subyacentes, lo cual sugiere que tiene un “sentido físico” mucho más profundo que las redes tradicionales.

Explorando simetrías y estructuras ocultas

Uno de los aspectos más llamativos del artículo es el uso de las KANs para identificar estructuras internas complejas y simetrías ocultas en los datos, incluso cuando estas no son evidentes a simple vista. En física, las simetrías suelen estar asociadas a leyes fundamentales de conservación. Encontrarlas es, muchas veces, una tarea larga y compleja.

En un experimento avanzado, una KAN fue capaz de reproducir —sin conocimiento previo— el resultado de un artículo técnico de 17 páginas sobre las simetrías de los agujeros negros de Kerr. Esto demuestra que el modelo puede, a partir de los datos de entrada, construir representaciones que reflejan estructuras teóricas profundas.

Según los autores, “KANs permiten descubrir simetrías no triviales directamente desde los datos sin necesidad de intervención humana”. Este hallazgo plantea una posibilidad interesante: que las redes neuronales puedan servir como una nueva herramienta exploratoria en física teórica, capaz de encontrar patrones que incluso los humanos han pasado por alto.

Más allá de la predicción: comprensión modular

Otro avance clave presentado por las KANs es su capacidad para aprender representaciones modulares, es decir, estructuras internas que pueden reutilizarse en distintos contextos. Esta característica se aleja de la lógica opaca de muchas redes neuronales actuales, acercándose más a cómo los humanos comprenden y organizan el conocimiento.

En los experimentos realizados, las KANs aprendieron funciones complejas descomponiéndolas en bloques reutilizables, lo que sugiere una forma de razonamiento más eficiente. Según el artículo, “los componentes aprendidos por una KAN pueden transferirse a nuevas tareas con modificaciones mínimas”. Este tipo de aprendizaje modular podría facilitar avances en múltiples áreas de la ciencia aplicada, desde la química hasta la biomecánica.

Además, los investigadores destacan que las funciones aprendidas por las KANs pueden visualizarse de forma clara, lo que permite inspeccionar los pasos intermedios del razonamiento del modelo. Esta transparencia refuerza su valor como herramienta científica.

KANs como herramienta de descubrimiento científico

En lugar de limitarse a resolver problemas definidos, las KANs están pensadas para explorar lo desconocido. En el artículo, los autores enfatizan que su arquitectura puede integrarse en procesos científicos para ayudar a formular hipótesis, verificar leyes emergentes y entender fenómenos complejos.

La capacidad de extraer fórmulas simbólicas interpretables convierte a las KANs en candidatas ideales para reemplazar métodos tradicionales de ajuste de curvas o análisis de regresión. También pueden integrarse en entornos donde se requiere explicabilidad, como en medicina o ingeniería.

Además, las KANs tienen una ventaja práctica: requieren menos parámetros que las redes neuronales estándar, lo que las hace más eficientes desde el punto de vista computacional. Esta eficiencia, combinada con su capacidad interpretativa, las posiciona como una opción prometedora para acelerar el proceso de descubrimiento en ciencias naturales y aplicadas.

¿Un nuevo tipo de inteligencia científica?

El desarrollo de las KANs plantea una pregunta provocadora: ¿estamos ante una forma de inteligencia artificial capaz no solo de imitar al científico humano, sino de complementarlo e incluso superarlo en ciertas tareas? Al permitir el descubrimiento de leyes sin intervención explícita, este modelo redefine el papel de la IA en la ciencia.

A diferencia de otros enfoques, que requieren grandes cantidades de datos y dependen de ajustes empíricos, las KANs se acercan más a una intuición matemática, operando sobre estructuras funcionales en lugar de mapas de correlación. Como explican los autores, su arquitectura “combina la expresividad de las redes neuronales con la claridad del razonamiento simbólico”.

Esto no significa que reemplacen al pensamiento humano, pero sí que pueden ampliar sus capacidades. La ciencia moderna se enfrenta a cantidades masivas de datos que superan la capacidad de análisis humano. Modelos como las KANs pueden actuar como brújula, guiando a los investigadores hacia patrones y estructuras que valdría la pena explorar más a fondo.

Cortesía de Muy Interesante

Dejanos un comentario: