Intentemos hacer el esfuerzo de imaginar una cuerda que se anuda en formas complejas, como un lazo que nunca se deshace, y que las matemáticas que describen esos nudos fueran esenciales para construir ordenadores del futuro. Por improbable que suene, eso es exactamente lo que un grupo de científicos ha demostrado. Al unir conceptos de la física cuántica, la matemática de los nudos y la tecnología avanzada, un equipo de investigación ha dado un paso importante hacia la estabilización de las computadoras cuánticas, lo que promete resolver algunos de sus problemas más complejos.
En su estudio, publicado en Physical Review Letters y liderado por Jia-Kun Li y sus colegas, los investigadores lograron calcular los polinomios de Jones, herramientas matemáticas clave para describir nudos, mediante el uso de modos de Majorana. Este avance no solo representa una conexión inédita entre disciplinas, sino que también tiene el potencial de revolucionar la tecnología cuántica al mejorar su estabilidad y eficiencia. Lo interesante es que este avance combina elementos aparentemente desconectados, como las propiedades de partículas cuánticas y las características de los nudos topológicos, para resolver uno de los grandes retos tecnológicos de nuestro tiempo.
¿Qué son los modos de Majorana y por qué son importantes?
Los modos de Majorana son un tipo especial de cuasipartícula que ha fascinado a los físicos desde hace décadas. A diferencia de la mayoría de las partículas, que tienen una antipartícula correspondiente (como el electrón y el positrón), las partículas de Majorana son su propia antipartícula. Esta peculiaridad las hace especialmente útiles en el campo de la computación cuántica. La hipótesis de su existencia se remonta a 1937 y se debe al físico italiano Ettore Majorana.
Una de las características más importantes de los modos de Majorana es su resistencia a interferencias externas. En las computadoras cuánticas convencionales, los qubits (las unidades básicas de información cuántica) son increíblemente frágiles. Pueden perder su estado debido a factores como el ruido ambiental o las vibraciones, introduciendo errores que dificultan los cálculos. Los modos de Majorana, por el contrario, tienen una propiedad única: cuando se trenzan o entrelazan, su estado cuántico queda protegido contra estas interferencias. Esto es lo que los hace ideales para la llamada computación cuántica topológica.
En la computación cuántica topológica, la información no depende de las características específicas del entorno, sino de la estructura general de cómo están dispuestas las partículas. Esto significa que, aunque una partícula individual sea afectada por ruido, el “nudo” completo de información permanece intacto. Este enfoque promete mayor estabilidad y una reducción significativa en los sistemas de corrección de errores, lo que podría hacer que las computadoras cuánticas sean mucho más eficientes.

Los polinomios de Jones y su conexión con los nudos
Antes de profundizar en la conexión entre estas partículas y los nudos, es importante entender qué son los polinomios de Jones. En matemáticas, los nudos son objetos fascinantes que pueden describirse mediante fórmulas específicas que capturan sus propiedades. Uno de estos métodos es el polinomio de Jones, una herramienta matemática que actúa como una “huella digital” de un nudo, lo que nos permite distinguir entre diferentes tipos de nudos y enlaces. Los polinomios de Jones fueron descubiertos por el matemático neozelandés Vaughan Jones en 1984.
Los polinomios de Jones tienen aplicaciones en múltiples campos, desde la biología molecular, donde ayudan a analizar el entrelazado del ADN, hasta la física teórica, donde describen las propiedades de los sistemas topológicos. Sin embargo, calcular estos polinomios puede ser extremadamente complicado. Para algunos tipos de nudos, los cálculos requieren una cantidad de recursos computacionales que crece exponencialmente con la complejidad del nudo. Es aquí donde la computación cuántica, con su capacidad de procesar grandes cantidades de información simultáneamente, entra en escena.
El avance del equipo de investigación
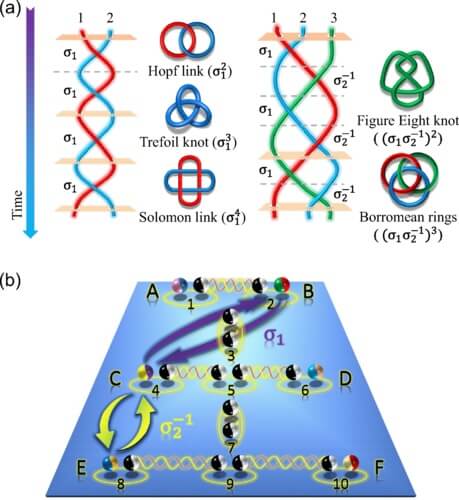
El equipo de Jia-Kun Li logró usar un simulador cuántico fotónico para calcular los polinomios de Jones de varios nudos topológicos. Este simulador utilizó haces de luz láser, distribuidos en un sistema de interferometría óptica, para simular el trenzado de modos de Majorana. Cada operación de trenzado correspondía a un enlace topológico específico, y al medir las propiedades de estos enlaces, los investigadores pudieron determinar los polinomios de Jones asociados. Según el estudio, esta metodología demostró una fidelidad del 97 % en las simulaciones realizadas, lo que confirma la viabilidad del enfoque.
Este avance establece una base sólida para futuras investigaciones en computación cuántica topológica. Los resultados del equipo demuestran que es posible utilizar modos de Majorana y simuladores cuánticos para realizar cálculos que serían prohibitivos para las computadoras clásicas. Por otra parte, el uso de sistemas ópticos para estas simulaciones abre la puerta a dispositivos más eficientes y escalables en el futuro.

Unas propiedades ideales para ser aplicadas
La utilidad de los modos de Majorana en este contexto radica en su capacidad para resistir interferencias externas y mantener la integridad de la información cuántica. Cuando estas partículas se trenzan, forman estructuras topológicas que son intrínsecamente estables. Este comportamiento es similar al de un nudo en una cuerda: aunque demos un tirón de un extremo o modifiquemos la forma externa, el nudo en sí mismo permanece intacto. Esta estabilidad es crucial para la computación cuántica, ya que permite realizar cálculos complejos sin que los errores acumulados comprometan el resultado final.
Además de mejorar la estabilidad de las computadoras cuánticas, este avance tiene implicaciones potenciales en otros campos científicos. Por ejemplo, en biología molecular, donde los nudos topológicos son comunes en el ADN, estas técnicas podrían facilitar el estudio de las propiedades físicas y químicas de las moléculas. Asimismo, en física de materiales, la capacidad de simular sistemas topológicos complejos podría acelerar el desarrollo de nuevos materiales con propiedades únicas.
Este avance representa un paso significativo hacia la construcción de computadoras cuánticas más prácticas y robustas. Sin embargo, todavía quedan muchos retos por resolver. Por ejemplo, aunque los simuladores cuánticos fotónicos han demostrado ser efectivos para estudiar sistemas pequeños, escalar estos dispositivos para manejar problemas más grandes y complejos sigue siendo un desafío. A pesar de ello, los resultados obtenidos hasta ahora muestran un camino prometedor hacia el futuro de la computación cuántica.
Referencias
- Jia-Kun Li et al., Photonic Simulation of Majorana-Based Jones Polynomials, Physical Review Letters, vol. 133, no. 23, 2024. DOI: 10.1103/PhysRevLett.133.230603.
Cortesía de Muy Interesante
Dejanos un comentario: