Resolver crucigramas puede parecer una actividad cotidiana, pero para la física, estos rompecabezas esconden una fascinante complejidad. ¿Qué pasa cuando, tras varios minutos de estancamiento, una palabra clave desbloquea todo el tablero? Este fenómeno, familiar para quienes disfrutan de estos juegos, inspiró al físico Alexander K. Hartmann, de la Universidad de Oldenburg, a desarrollar un modelo matemático que conecta la resolución de crucigramas con la teoría de la percolación, una herramienta fundamental en la física estadística.
En su artículo publicado en Physical Review E, Hartmann describe cómo los crucigramas pueden estudiarse como sistemas en transición entre orden y caos. Su modelo analiza cómo pequeñas pistas parciales pueden llevar a un “efecto dominó”, donde resolver una palabra facilita la solución de otras. La investigación no solo aporta un enfoque novedoso al análisis de redes, sino que también explora cómo conceptos físicos pueden aplicarse a fenómenos cotidianos como los crucigramas.
¿Qué es la percolación y por qué importa en este contexto?
La percolación es un fenómeno que describe cómo un sistema conectado pasa de un estado fragmentado a uno continuo. Imagina que unas gotas de agua comienzan a filtrarse a través de una esponja seca: al principio, el agua solo humedece algunas partes, pero al alcanzar cierto punto crítico, el líquido se distribuye por toda la esponja. Este concepto, común en física, puede aplicarse a redes sociales, estructuras urbanas e incluso a sistemas biológicos.
Hartmann sugiere que un crucigrama funciona de forma similar. Las casillas blancas y negras representan un sistema en el que las “conexiones” ocurren al resolver palabras. Cuando un jugador completa una palabra, adquiere conocimiento parcial que le permite resolver palabras cercanas, creando lo que en física se llama un “camino de percolación”. Este proceso, según el autor, puede modelarse matemáticamente para estudiar los puntos críticos que llevan a resolver un rompecabezas completo.

Dos modelos: iid y game variant
En el artículo, Hartmann introduce dos variantes de su modelo de percolación: iid (independientemente distribuido) y game variant (variante de juego). Cada uno simula un enfoque diferente de cómo los jugadores resuelven crucigramas:
- Modelo iid: Aquí, cada casilla blanca del crucigrama tiene una probabilidad fija de estar ocupada por una letra correcta, sin depender de otras casillas. Este modelo es útil para compararlo con la percolación clásica, ya que sigue principios estándar de probabilidad.
- Modelo game variant: En este enfoque, la probabilidad de resolver una palabra aumenta si comparte casillas con palabras ya resueltas. Esto refleja la experiencia real de los jugadores, donde una pista parcial puede desbloquear nuevas conexiones. Según Hartmann, este modelo introduce correlaciones dinámicas, lo que lo hace más complejo y relevante para sistemas reales.
Un hallazgo clave del estudio es que el modelo game variant exhibe un comportamiento distinto al de la percolación tradicional. Como señala el autor, los exponentes críticos, como el de la longitud de correlación, no son universales y dependen de cómo se acelera la solución de palabras cruzadas.
Transiciones críticas y avalanchas
Un concepto interesante que emerge del trabajo de Hartmann es el de las transiciones de fase. Al igual que el agua pasa de sólido a líquido en condiciones específicas, un crucigrama puede pasar de “incompleto” a “completado” una vez que se alcanza un nivel crítico de conocimiento parcial.
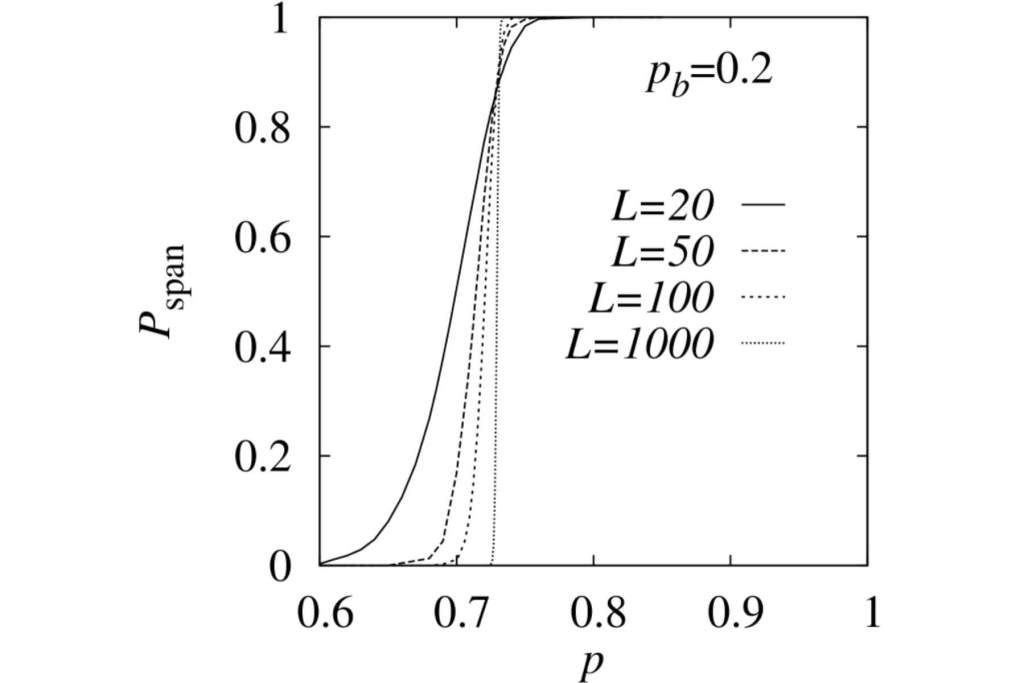
Hartmann describe este cambio como un fenómeno similar a una avalancha: resolver una palabra genera una cascada de soluciones adicionales, acelerando la resolución del crucigrama. Este comportamiento puede analizarse utilizando simulaciones por computadora. Los resultados muestran que, en el modelo game variant, las transiciones son más bruscas y dependen del nivel de conocimiento inicial y de cómo se propaga la información a través del tablero.
Las simulaciones, realizadas en redes de distintos tamaños, confirman que el modelo tiene aplicaciones más allá de los crucigramas. Según el autor, este enfoque podría extenderse a redes sociales o sistemas de información, donde pequeños cambios pueden desencadenar impactos significativos.

Mucho más que un pasatiempo
El trabajo de Hartmann no solo abre una nueva línea de investigación en física estadística, sino que también plantea preguntas interesantes. Por ejemplo, ¿pueden estos modelos predecir cómo se propagan las ideas en una red social? ¿Qué ocurre cuando el “beneficio” de resolver una palabra parcial es menor o mayor?
Por otra parte, el estudio sugiere que este tipo de percolación dinámica podría estar relacionado con fenómenos como la autoorganización crítica, donde los sistemas se ajustan naturalmente hacia un estado límite entre el orden y el caos. Sin embargo, aún queda mucho por explorar, como estudiar cómo se comporta el modelo en tres dimensiones o determinar si los hallazgos se mantienen en sistemas más complejos.
Referencias
Cortesía de Muy Interesante
Dejanos un comentario: