La mayoría de nosotros la aprendimos en la escuela como una fórmula mágica. Nos la enseñaron como algo que simplemente “es”, como un truco poderoso que resuelve cualquier ecuación de segundo grado. Igual nunca nos dijeron que se llama “fórmula de Bhaskara”. O sí, porque hay quien le asigna a Bhaskara su origen. Pero ¿realmente fue Bhaskara quien la descubrió? ¿Es tan moderna como parece? ¿De dónde viene esa elegante combinación de símbolos y raíces cuadradas?
La historia de esta fórmula es mucho más antigua, rica y fascinante de lo que podrías imaginar. Involucra a babilonios que resolvían problemas con arcilla, sabios indios que escribían en verso, matemáticos islámicos que fundaron el álgebra, y europeos que finalmente la transformaron en lo que conocemos hoy. Esta es la verdadera historia de la solución de las ecuaciones de segundo grado. Obviamente, antes de continuar, deleitémonos con su formulación, que nos lleva a nuestros años de secundaria:
Un problema con miles de años
Resolver ecuaciones de segundo grado —es decir, aquellas que tienen la forma ax2+bx+c=0— puede parecer un ejercicio de álgebra moderna. Pero su origen se remonta a más de 4.000 años, cuando las primeras civilizaciones del mundo empezaban a dejar registros de su pensamiento matemático.
Babilonia: soluciones sin fórmulas
Los babilonios, hacia el 2000 a.C., ya sabían resolver problemas que hoy en día traduciríamos como ecuaciones cuadráticas. No usaban letras ni símbolos algebraicos, y desde luego no tenían una fórmula general, pero sí métodos numéricos efectivos.
Por ejemplo, sabían que si una cierta cantidad más su cuadrado sumaban un número dado, podían hallar la cantidad aplicando lo que hoy llamamos “completar el cuadrado”. Trabajaban con tablas de cuadrados y raíces, y resolvían ecuaciones como:
“El producto de una cantidad con ella misma, sumado a diez veces la cantidad, da 39; ¿cuál es la cantidad?”
Lo resolvían paso a paso, a través de procedimientos aritméticos y geométricos, en tabletas de arcilla escritas en cuneiforme.
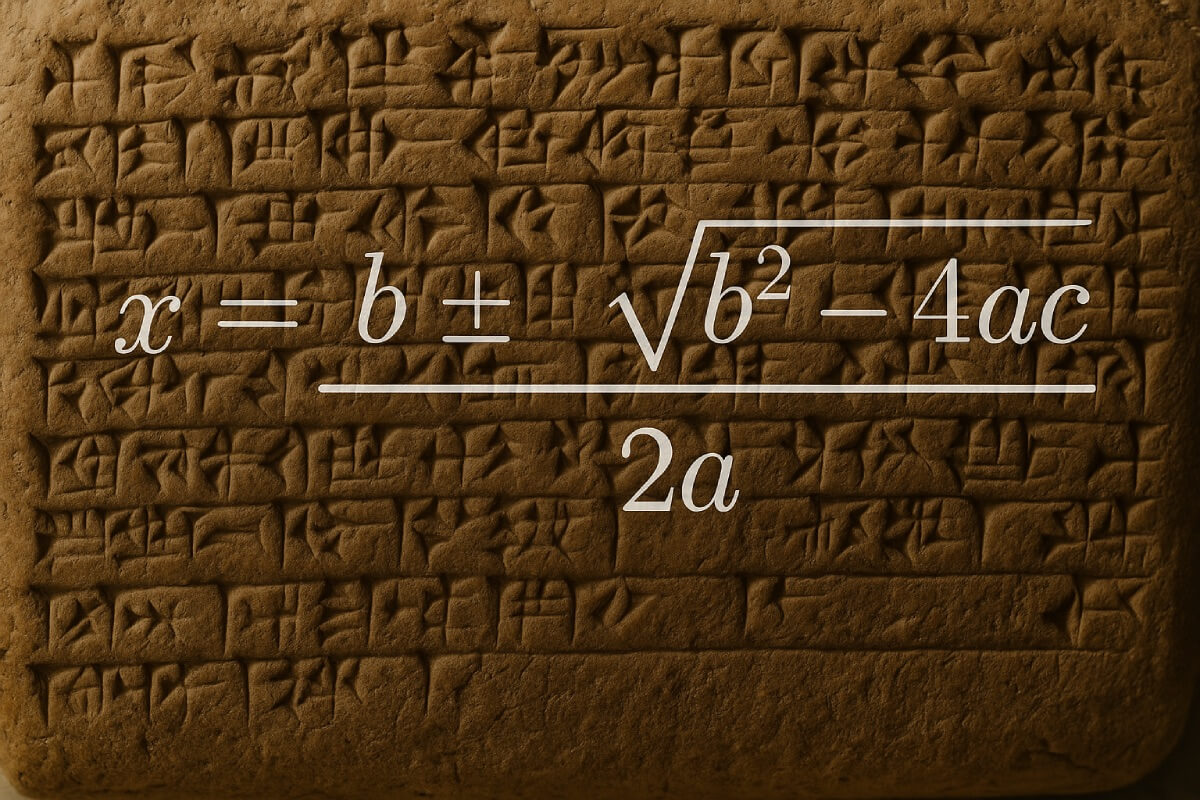
De la geometría griega al verso indio
Mientras los griegos preferían los razonamientos geométricos abstractos, en la India y en el mundo islámico comenzó a florecer el álgebra tal como lo entendemos hoy.
Brahmagupta: la abstracción de lo negativo
En el siglo VII, el matemático indio Brahmagupta ya trabajaba con ecuaciones cuadráticas, e incluso aceptaba soluciones negativas, algo revolucionario para la época. Su obra Brahmasphutasiddhanta contenía reglas para resolver lo que hoy escribiríamos como:
o incluso con términos negativos. Era un paso esencial hacia la abstracción del álgebra.
Bhaskara II: la fórmula en forma poética
Bhaskara II, en el siglo XII, abordó la resolución de ecuaciones cuadráticas utilizando el método de completar el cuadrado, una técnica ya extendida en la matemática india de la época. En su obra Lilavati, escrita en verso y pensada como manual didáctico, plantea problemas que implican la resolución de este tipo de ecuaciones, aunque no presenta la fórmula cuadrática general tal como la conocemos hoy. La exposición es más algorítmica que simbólica, y aunque algunos autores han interpretado sus versos como una versión poética de dicha fórmula, no se conserva una expresión literal que la enuncie explícitamente.
Aunque no con símbolos, el razonamiento era claro. Por eso, en muchos países la fórmula lleva su nombre: “fórmula de Bhaskara”.

El álgebra toma forma: Al-Juarismi y el legado islámico
Al mismo tiempo, en el siglo IX, el matemático persa Al-Juarismi escribió un tratado fundamental llamado Al-Kitab al-Mukhtasar fi Hisab al-Jabr wa’l-Muqabala, que significa “Compendio sobre cálculo por completación y balanceo”. De ahí proviene la palabra “álgebra”.
Al-Juarismi resolvía sistemáticamente ecuaciones cuadráticas completando el cuadrado, pero sin símbolos, y solo con soluciones positivas (los números negativos aún no eran aceptados en general). Usaba casos como:
y mostraba cómo convertirlo en un cuadrado perfecto:
La solución, por tanto, era
Este método es el corazón de la deducción moderna de la fórmula.
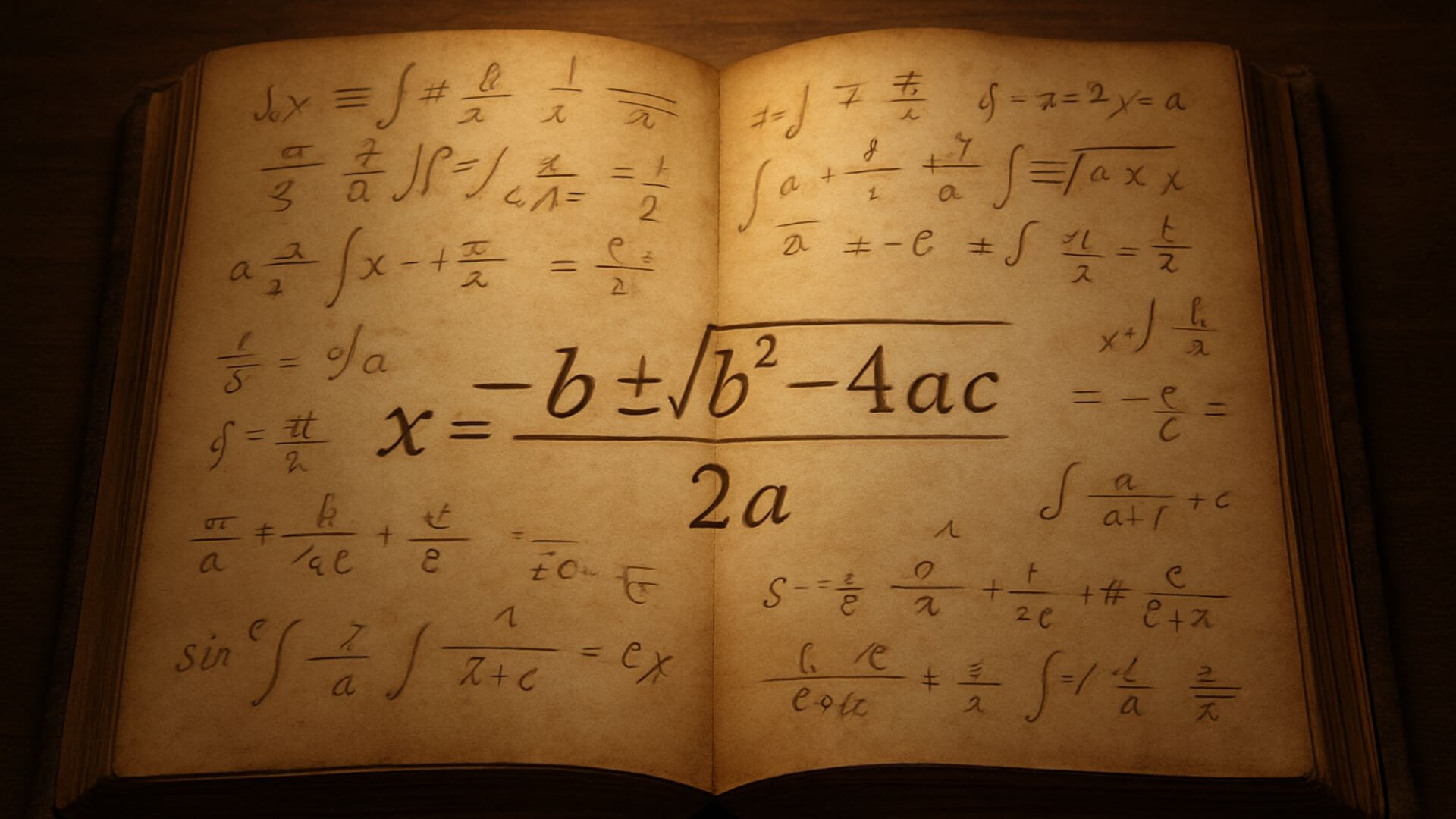
La fórmula moderna: Europa y la notación simbólica
No fue hasta los siglos XV y XVII que Europa comenzó a usar la notación algebraica que nos resulta familiar. Figuras como François Viète y René Descartes introdujeron el uso sistemático de letras para incógnitas y coeficientes.
En este contexto, finalmente la fórmula cuadrática apareció escrita tal como la conocemos hoy, con letras y signos:
No fue un descubrimiento nuevo, sino una formalización simbólica de ideas que ya existían desde hacía siglos. Pero el poder del símbolo lo cambió todo: ahora la solución podía enseñarse y usarse de forma universal.
¿Cómo se deduce esta fórmula?
El razonamiento detrás de la fórmula se basa en el método de completar el cuadrado, tal como lo usaban los babilonios y Al-Juarismi. Aquí va una demostración breve:
- Partimos de la ecuación general:
- Dividimos todo entre a:
- Completamos el cuadrado sumando a ambos lados el cuadrado del término (b/2a)
- El lado izquierdo es un trinomio cuadrado perfecto:
Extraemos raíz y despejamos. Ojo, porque debemos poner dos subíndices, 1 y 2, para denotar con claridad que son dos posibles soluciones:
Y así, como por arte de magia… pero con pura lógica algebraica, surge la fórmula universal.
Aplicaciones reales de la fórmula cuadrática
Lejos de ser una curiosidad matemática, esta fórmula aparece en contextos muy variados:
- Física: cálculo de trayectorias en el tiro parabólico, puntos de caída, velocidad.
- Economía: modelos de beneficio y pérdida donde se optimizan funciones cuadráticas.
- Ingeniería: diseño de estructuras, sistemas de control, análisis de señales.
- Arte y música: modelado de curvas, análisis armónico.
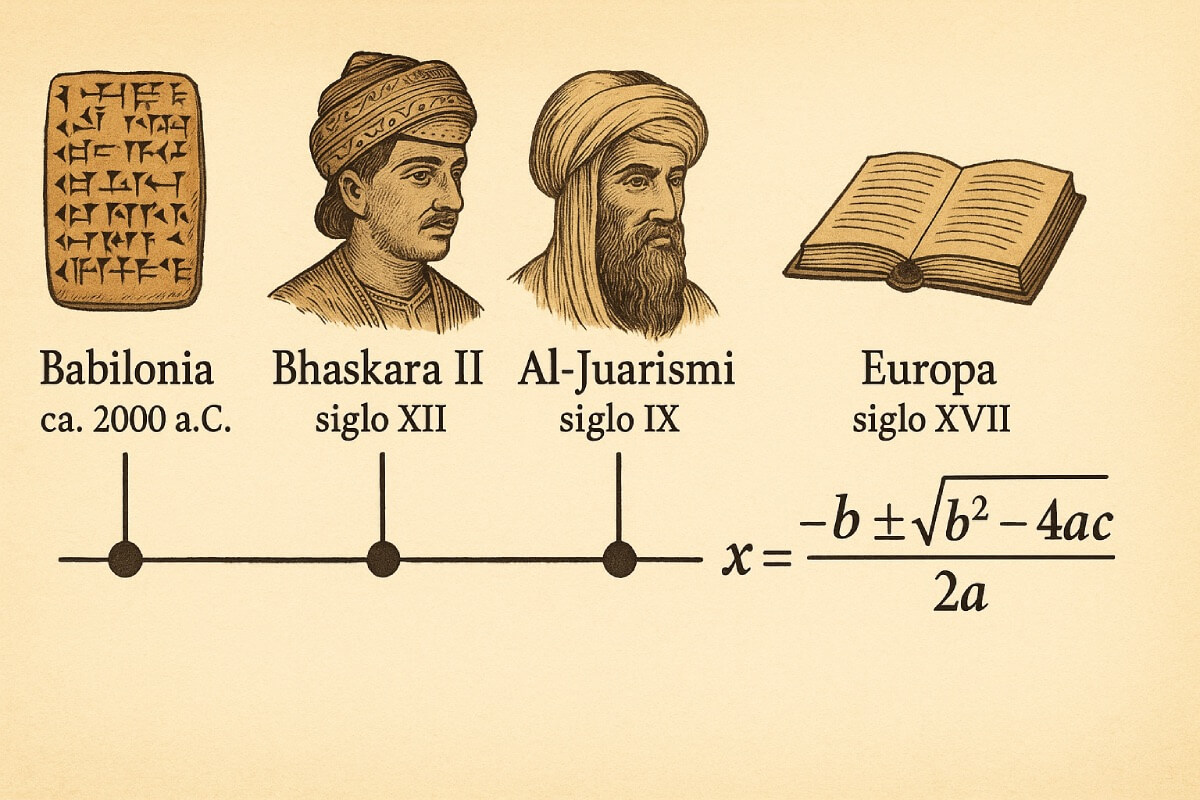
¿Entonces… fue Bhaskara?
La fórmula que usamos hoy lleva el nombre de Bhaskara II en muchos países, sobre todo en América Latina y Brasil. Pero la verdad es que no fue su descubrimiento exclusivo, ni fue el primero en resolver ecuaciones cuadráticas.
La historia muestra que fue una construcción colectiva, una evolución que cruzó culturas, continentes y siglos. Los babilonios plantearon el problema, los indios y musulmanes desarrollaron métodos, y los europeos refinaron la notación.
Llamarla “fórmula de Bhaskara” es una forma conveniente de recordar uno de los momentos clave en esta larga historia, pero no hace justicia al esfuerzo compartido de muchas civilizaciones.
Cortesía de Muy Interesante
Dejanos un comentario: