Físicos encuentran una regla que todos los mercados financieros siguen, sin excepción

¿Qué tienen en común las acciones de Toyota, el bitcoin, el petróleo y los mercados de divisas? Más allá de sus diferencias, todos obedecen una misma ley matemática cuando son comprados o vendidos en grandes cantidades. No se trata de una conjetura, ni de una regla práctica sacada de manuales de inversión. Es una ley empírica rigurosa, probada con datos reales y masivos, que describe cómo varían los precios según la cantidad negociada.

En diciembre de 2025, los investigadores Yuki Sato y Kiyoshi Kanazawa publicaron una prueba definitiva de esa ley, conocida como la ley de la raíz cuadrada del impacto del precio. Lo hicieron tras analizar millones de transacciones en la Bolsa de Tokio durante ocho años, una hazaña sin precedentes en el campo de la econofísica. Como explican, “el exponente δ es igual a 1/2 dentro de los errores estadísticos, tanto a nivel de acciones individuales como de operadores individuales”. Esta frase encierra un hallazgo que podría cambiar la manera en que entendemos los mercados financieros.

Qué es exactamente la ley de la raíz cuadrada

En palabras sencillas, esta ley establece que el precio de un activo no cambia proporcionalmente a la cantidad comprada o vendida. Es decir, si se compra el doble de acciones, el precio no sube el doble, sino una cantidad menor, concretamente proporcional a la raíz cuadrada del volumen negociado. Por ejemplo, si comprar el 1 % del volumen diario de una acción mueve su precio un 10 %, comprar el 4 % movería el precio un 20 %, no un 40 %.

Este fenómeno, documentado durante años en distintos mercados, no había sido probado de forma concluyente como una ley universal. Había estudios previos, pero se basaban en datos parciales, restringidos a ciertos operadores o instrumentos financieros. Además, el análisis era a menudo poco preciso o limitado por el acceso a información privada.

El avance de Sato y Kanazawa consiste en demostrar que la ley se cumple de forma sistemática para más de 2.000 acciones, y también para más de 1.200 operadores individuales, con un margen de error estadístico extremadamente bajo. Eso convierte a la ley en una candidata firme para considerarse una regla universal del comportamiento de los mercados.

Cómo se hizo el estudio: ocho años, millones de órdenes

Para llegar a estas conclusiones, los investigadores utilizaron un conjunto de datos proporcionado por el Japan Exchange Group, que gestiona la Bolsa de Tokio. Esta base incluía todas las órdenes de compra y venta, con un nivel de detalle suficiente como para reconstruir el comportamiento de cada operador a lo largo del tiempo.

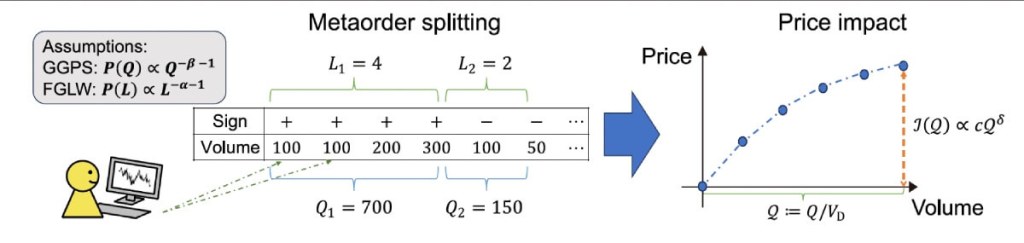
Una de las claves del análisis fue identificar las llamadas “metaórdenes”: grandes operaciones que los inversores institucionales dividen en muchas órdenes pequeñas para no alterar demasiado el mercado. Al estudiar cómo estas metaórdenes afectan al precio, se puede medir con precisión el impacto del precio (Δp) en función del volumen negociado (Q).

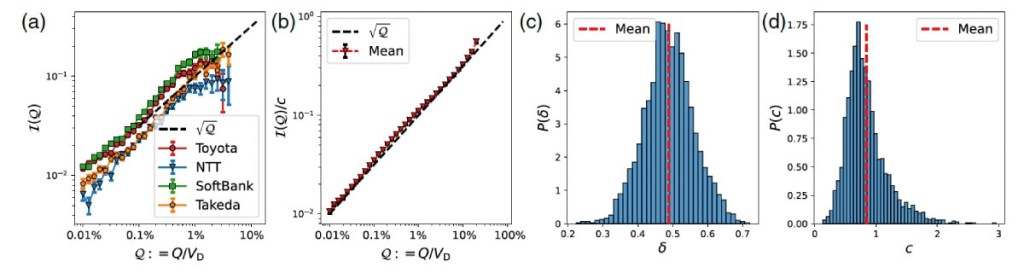
Los autores agruparon y normalizaron los datos usando parámetros diarios (como la volatilidad y el volumen total negociado) y aplicaron técnicas estadísticas avanzadas para estimar el exponente δ de la ley. El resultado fue una distribución con un pico nítido en 0,5, con una desviación estándar de apenas 0,071, lo que demuestra la consistencia del fenómeno.

¿Qué significa que sea una ley universal?

En física, una ley es universal cuando se cumple en distintos sistemas, sin depender de detalles microscópicos. El ejemplo clásico es la ley de los gases o la ley de la gravedad. En este caso, la ley de la raíz cuadrada describe cómo se comporta un mercado sin importar qué acción se negocie, qué empresa esté detrás o quién compre o venda.

Sato y Kanazawa lograron demostrar que la misma relación matemática se cumple para todos los activos estudiados, y también para todos los operadores activos que realizaron más de 10.000 operaciones. Esta es la primera vez que se demuestra este nivel de universalidad en un fenómeno financiero.

Esto tiene implicaciones importantes: si los mercados obedecen esta ley, se pueden diseñar modelos más precisos para prever sus movimientos. También se pueden mejorar los algoritmos de inversión, que hoy ya dominan gran parte de las operaciones bursátiles. Y sobre todo, permite entender mejor cómo pequeñas decisiones pueden generar grandes oscilaciones en los precios.

La fórmula que lo resume todo

El hallazgo de Sato y Kanazawa se resume en una ecuación sencilla, pero con implicaciones profundas. Se trata de una ley empírica que describe cuánto cambia el precio de un activo financiero cuando se compra o vende una cierta cantidad de ese activo. La fórmula es:

$$I(Q)=c\cdot Q^{1\mathrm{/}2}$$

• I(Q) representa el impacto medio en el precio, es decir, cuánto sube o baja el precio después de ejecutar una orden de volumen $Q$Q.
• Q es el volumen de la operación, expresado en relación con el volumen total negociado ese día.
• c es un coeficiente de escala que depende del activo y su volatilidad, pero no modifica la forma de la ley.

La clave está en el exponente 1/2. Esto significa que el impacto del precio no crece de manera proporcional al volumen, sino más lentamente. Por ejemplo, duplicar el tamaño de una operación solo aumenta el impacto en un 41 %, no al doble. Esa relación es lo que se conoce como ley de la raíz cuadrada del impacto del precio, y el estudio demuestra que se cumple con una precisión estadística extraordinaria en miles de casos.

Volviendo a lo que firman los autores, “el exponente δ es igual a 1/2 dentro de los errores estadísticos, tanto a nivel de acciones individuales como de operadores individuales”.

Modelos descartados y teoría alternativa

Hasta ahora, había dos teorías principales que explicaban por qué el impacto del precio podía no ser universal. Una era el modelo GGPS, que relaciona el impacto con el tamaño de las órdenes, y otra el modelo FGLW, que lo vincula con la forma en que se dividen las operaciones. Ambas predecían que el exponente δ podía variar según las condiciones del mercado.

Sato y Kanazawa pusieron a prueba estas teorías midiendo los parámetros de cada modelo con sus datos. El resultado fue claro: no había correlación entre esos parámetros y el valor de δ. Es decir, ambas teorías fallaban en predecir el comportamiento observado en la Bolsa de Tokio. Esto refuerza la idea de que estamos ante un fenómeno universal, no condicionado por factores particulares.

Por otro lado, hay un modelo que sí parece alinearse con los datos: la teoría de la liquidez latente, propuesta en trabajos anteriores por Jean-Philippe Bouchaud y colaboradores. Según este enfoque, la cantidad de órdenes disponibles aumenta con la distancia respecto al precio actual, lo que genera una resistencia creciente a cambios de precio. Esa resistencia explicaría la forma de la ley observada, donde el impacto crece con la raíz cuadrada del volumen.

Por qué este hallazgo importa (mucho más de lo que parece)

Los mercados financieros son sistemas complejos, con miles de agentes interactuando en tiempo real. A pesar de esta complejidad, el descubrimiento de una ley como esta muestra que es posible encontrar regularidades matemáticas profundas en el caos aparente. No es solo una curiosidad teórica: entender cómo se transmiten las decisiones individuales al comportamiento colectivo puede ayudar a prevenir crisis y a mejorar la estabilidad del sistema financiero.

Además, este estudio marca un hito metodológico. Nunca antes se había analizado un mercado entero con tanta precisión, a lo largo de tantos años y con un nivel de detalle que permite seguir cada operación hasta su origen. Esto abre la puerta a nuevos estudios similares en otros mercados, como Wall Street o el Nasdaq, para confirmar si la ley también se cumple allí.

El impacto potencial va más allá del mundo académico. Las agencias reguladoras, los bancos centrales, los fondos de inversión y hasta los desarrolladores de inteligencia artificial para trading pueden usar este conocimiento para tomar decisiones más informadas. En un mundo donde los mercados globales están interconectados y reaccionan con velocidad, comprender cómo se propagan los impactos de cada operación es más relevante que nunca.

Cortesía de Muy Interesante

Dejanos un comentario: