Salgo del metro en la estación de Retiro. Llego tarde –para variar– y no tengo claro dónde he quedado con mi hermana. Abro nuestro chat en la aplicación de mensajería instantánea. Fuente del Ángel Caído. He ido mil veces, pero aun así tecleo el lugar en la aplicación de mapas de mi móvil, para que esta me sugiera el camino más rápido. 17 minutos, pasando por detrás del estanque y del Palacio de Cristal. Lo tengo. Voy volando.
Para dar respuesta a esta cuestión, de apariencia sencilla, la aplicación de mapas ha empleado diversa tecnología, basada fundamentalmente en conceptos matemáticos –casi todo son matemáticas en la sociedad de las comunicaciones–. Uno de los ingredientes principales es una estructura llamada grafo, cuya formulación se remonta al siglo xviii. Su uso actual en problemas que surgen de las ciencias de la computación le otorga más vigencia que nunca. «Hoy en día estamos rodeados de grafos. Una de las aplicaciones que usamos día tras día es la consulta de mapas online, que se basan en algoritmos de búsqueda de caminos mínimos en grafos». Habla Juanjo Rué, experto en teoría de grafos, profesor agregat de la Universidad Politécnica de Cataluña e investigador del Centre de Recerca Matemàtica.
Uno de estos algoritmos es el algoritmo de Dijkstra, ideado en 1956 por Edsger Dijkstra, uno de los fundadores de la computación moderna, entonces programador del Centrum Wiskunde & Informatica (CWI) de Amsterdam.
Un objeto matemático para describir relaciones
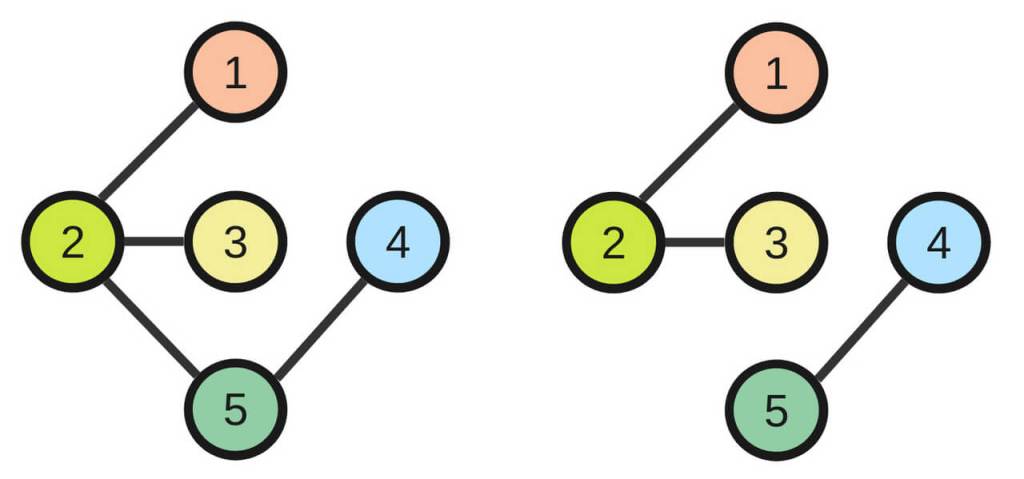
Empecemos por el principio: un grafo es un objeto matemático que permite describir de forma sencilla cierta relación entre elementos –conexiones, dependencia o interacciones–. Está formado por dos tipos de elementos: una colección de puntos, que se denominan vértices –o nodos–, y uniones entre ellos, que reciben el nombre de aristas. En sus aplicaciones más populares, los nodos representan personas y los vértices conectan a aquellas que son amigas en determinada red social –voilá, el grafo es un modelo de Facebook–; en su uso en los mapas digitales, las aristas representan fragmentos de calle, mientras que los vértices son las intersecciones, los puntos donde es posible elegir qué camino tomar. Esta es la descripción perfecta para analizar la navegación en la ciudad.
Para ello, se aplican herramientas matemáticas disponibles: teoremas sobre grafos desarrollados durante años. Estos establecen relaciones entre las características de un grafo, independientemente de qué grafo sea, o de si sus nodos representan personas o productos químicos. Es la belleza de las matemáticas. Una de las historias más contadas sobre teoría de grafos –la fundacional– es la del matemático Leonhard Euler que, para saber si era posible realizar un recorrido de cierto tipo en la ciudad de Königsberg, no solo dio con un nuevo teorema matemático, sino que inventó la teoría de grafos.
Euler definió el objeto matemático y dos de sus principales características: el grado y los caminos. El grado de un vértice es el número de aristas que lo conectan con otros vértices. En el grafo de los mapas digitales, la gran mayoría de nodos –intersecciones entre calles– tendrán grado cuatro, pero habrá otros, como una rotonda, que pueden tener un grado mayor, mientras que los cruces entre dos calles que suponen el final de una de ellas tendrán grado tres. El grado del grafo es la media de todos sus vértices. Ofrece una idea de cuán conectados están los elementos del grafo. En el mapa, será un valor cercano a cuatro –las intersecciones conectan habitualmente cuatro rutas–. En el caso de un grafo de las conexiones entre los aeropuertos europeos –formada por 377 nodos, los aeropuertos, y 3068 enlaces, que unen cada par de aeropuertos entre los que hay al menos un vuelo directo–, el grado es 16,2; es decir, de media cada aeropuerto está conectado con otros 16. Aunque la gran mayoría de ellos están muy lejos de la media: hay muchos, más del 30 %, con grado 1 o 2.
Por otro lado, un camino es una sucesión ordenada de vértices del grafo, en la que todos los nodos sucesivos están unidos por aristas. Si hay un camino entre el aeropuerto de Pula (Croacia) hasta el de Berlevag (Noruega), entonces es posible unir estos dos vértices, pasando por un número de vértices intermedios –Zadar, Zagreb, Zurich, Oslo, Alta y Mehamn–. En un grafo puede haber varios –o ningún– camino entre dos vértices. Si en el grafo cualquier par de vértices tienen un camino que los une, entonces es conexo. Es el caso de los aeropuertos europeos. Con mayor o menor número de escalas, siempre es posible unir cualquier par de aeropuertos. Euler probó que en cualquier grafo conexo existen caminos que empiezan en un punto, pasan por todas las aristas una única vez y vuelven al punto de partida si, y solo si, el grado de los vértices es par. Y, en el caso de Königsberg, como de alguna de las regiones salían tres puentes, no era posible recorrer todos los puentes de la ciudad una sola vez y volver al punto de inicio, que era el trayecto buscado.
A la caza del camino más corto
Muchos problemas con grafos tratan de localizar los caminos de menor longitud dentro de un grafo dado. La longitud es el número total de vértices de un camino. En el ejemplo de la conexión Pula-Berlevag, ocho. Y se trata de la opción con menos escalas, es decir, con menor tamaño. Pero también puede buscarse el camino que reduzca el gasto de combustible, es decir, con menos kilómetros de vuelo. Y para ello, habría que incluir en el grafo más información: se asigna a cada arista el número de kilómetros entre los dos aeropuertos que une. En otras ocasiones, interesa el camino cuyas conexiones suelen ser más baratas, de media. En este caso, se añade a cada arista la media de coste del vuelo que une esos dos aeropuertos. Estos valores numéricos que se atribuyen a cada arista se denominan pesos.
En las aplicaciones de mapas interesa saber cuánto se tarda en completar una ruta, por lo que, en cada arista, además de su longitud, se considera la velocidad de conducción permitida, el número de carriles, el tráfico habitual o la presencia de semáforos en ese fragmento de calle. Esta información se condensa en un peso, llamado «tiempo estimado de viaje». Para calcular el valor total de un trayecto se suman los pesos de todas las aristas del camino. Si el valor de un camino que une la estación del metro Retiro y la fuente del Ángel Caído es 25, significa que, de media, se tarda 25 minutos en recorrer ese trayecto. Y como ya sabemos desde el comienzo de esta lectura, hay caminos más cortos. El objetivo de la aplicación de mapas es encontrar el camino con la menor suma de los pesos de sus aristas.
Ahora bien, ¿cómo se localiza este camino? Una primera forma sería considerando todos los posibles caminos entre los dos puntos, calculando su peso, comparando todos estos valores y seleccionando el camino que tenga menor peso. Para resolver este tipo de preguntas sobre grafos grandes, hoy en día se emplean algoritmos, procesados por ordenadores, capaces de hacer cálculos sencillos de manera mucho más rápida que los humanos. Sin embargo, aun con ordenadores, el enfoque anterior implica un gran coste de tiempo y capacidad de cómputo. Por ello, se usan algoritmos como el de Dijkstra. «Es muy rápido, incluso en grafos con muchos vértices [como sucede en los mapas]. Si además el grafo tiene pocas aristas, el algoritmo es aún más veloz», afirma Rué.
Este algoritmo recorre todos los vértices del grafo, realizando cálculos y comparaciones sencillas en cada iteración. «Elige, en cada paso, la mejor decisión local: empieza por el vértice de origen y busca, entre sus vértices vecinos, el que tiene longitud mínima. A medida que explora más vértices, recuerda las selecciones anteriores y las va actualizando», explica Rué. Al concluir, ha obtenido el peso de los caminos mínimos que unen el vértice de partida con el resto de nodos del grafo, incluido el final. Esta información se emplea para construir el trayecto más rápido.
La comprensión de las grandes redes: uno de los principales retos
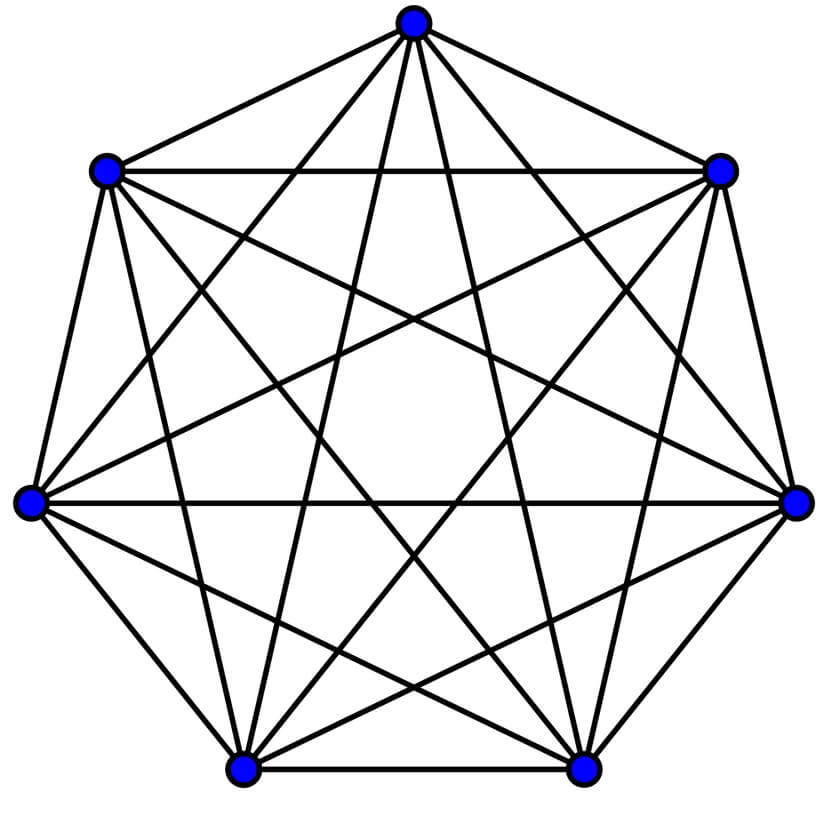
Sin embargo, si además de buscar el camino más corto, se quiere que este pase solo una vez por cada vértice y regrese al comienzo –para diseñar una ruta de un comercial que tiene que pasar por todas las ciudades de una zona, por ejemplo–, la cuestión se complica. «Es un problema muy parecido al de encontrar caminos mínimos entre dos nodos, pero muchísimo más difícil», afirma Rué. Para una red con un número pequeño de vértices y aristas, es posible hacer la cuenta a mano, pero la complejidad del problema crece rápidamente en cuanto este número aumenta. «Con unos pocos miles de vértices un ordenador tardaría posiblemente días o semanas en resolverlo. Con unos pocos millones, incluso utilizando ordenadores potentes, es impracticable», añade. Para Rué, la comprensión de las grandes redes y de su dinámica es uno de los grandes retos matemáticos de este momento. «El enorme tamaño de estos objetos hace que muchas veces, incluso teniendo herramientas computacionales muy potentes, no seamos capaces de resolver preguntas inocentes».
Este problema, conocido como el del viajante de comercio, es una de ellas. Es lo que se llama un problema NP completo, una clase de cuestiones de gran complejidad para las que no se dispone de un algoritmo eficiente que las resuelva. ahora bien, ante la dificultad de dar con el camino óptimo, se buscan buenas aproximaciones del mismo, que requieran mucho menos tiempo de cómputo.
«Si se busca una solución que no es óptima, pero cercana a serlo, por ejemplo, con una desviación del 2 % del valor óptimo real, podemos abordarlo para millones de vértices», afirma Rué. Recientemente, un grupo de investigadores lo hicieron para saber cuánto se tardaría en visitar –una única vez– las 2 079 471 estrellas catalogadas por el proyecto Gaia de la Agencia Espacial Europea. Su respuesta: 94 208 157,5 años luz. Para dar con esta ruta, utilizaron herramientas no solo de la teoría de grafos, sino también de la estadística y la probabilidad.
El enfoque probabilístico es cada vez más popular en la investigación sobre grafos. «En lugar de demostrar que un grafo cumple una propiedad, o no la cumple, de manera determinista [como hizo Euler con su teorema, que es una verdad absoluta que se cumple siempre], se intenta comprobar que, con una cierta probabilidad, dicha propiedad se satisface o no, lo que da lugar a procedimientos mucho más rápidos», reflexiona Rué. Por ejemplo, analizando una muestra más pequeña del grafo. «Gracias a las técnicas probabilísticas, podemos hacer afirmaciones globales a partir de información local», asegura.
Así, es posible analizar grafos inmensos que representan, por ejemplo, la estructura de la web (en este caso, donde las páginas son los nodos y los hipervínculos las aristas), una red social (digital o real), una red de telecomunicaciones, imágenes digitales… Como avisamos al comienzo del texto, hoy en día los grafos están en todas partes. Y, más allá de sus diversas aplicaciones, el área de la teoría de grafos es muy activa dentro de la investigación matemática. «En parte por la simplicidad de los problemas que se plantean, así como la dificultad de su resolución», concluye Rué.
Cortesía de Muy Interesante
Dejanos un comentario: