Por primera vez en la historia, un equipo internacional de físicos ha logrado medir directamente la geometría cuántica de los electrones dentro de un material sólido. Este avance, que parecía imposible hasta hace unos años, representa un salto revolucionario en el estudio de los materiales y de los fenómenos cuánticos. Dirigido por investigadores del MIT y la Universidad Nacional de Seúl, el experimento no solo ofrece un método completamente nuevo, sino que abre la puerta a explorar propiedades electrónicas con un nivel de detalle inédito. Posiblemente te estés preguntando qué es la “geometría cuántica de los electrones“. Es de lo que vamos a hablar en este artículo.
El paper, publicado recientemente en Nature Physics, presenta un enfoque experimental para medir una propiedad clave: el tensor geométrico cuántico (QGT). Este objeto matemático encapsula información esencial sobre cómo cambian los estados cuánticos y es una herramienta fundamental para comprender fenómenos topológicos. Según Riccardo Comin, físico del MIT y uno de los autores principales, “hemos desarrollado una hoja de ruta para obtener información completamente nueva que antes era inaccesible”. Este avance, aunque técnico, tiene implicaciones directas para diseñar materiales con propiedades únicas, como superconductores más eficientes o dispositivos electrónicos más avanzados.
Qué es la geometría cuántica y su importancia
Cuando los electrones se mueven en un material, no solo podemos pensar en ellos como pequeñas partículas. A nivel cuántico, se comportan como ondas. Estas ondas tienen una propiedad especial: ocupan un espacio, pero también tienen una forma matemática, como si trazaran un mapa en un espacio abstracto. A esta “forma” o “estructura” es lo que llamamos geometría cuántica. Una parte clave de esta descripción está en los orbitales electrónicos, que son regiones en las que es más probable encontrar al electrón dentro del material.
La geometría cuántica describe cómo cambia el estado de un electrón cuando experimenta pequeñas perturbaciones, como moverse dentro de un material o interactuar con campos magnéticos. Es como si pudiéramos medir cómo “curvada” o “diferente” es esa onda a medida que el electrón se desplaza. Para estudiar esta geometría, los físicos usan el tensor geométrico cuántico (QGT), que actúa como una especie de “herramienta de medición” que describe dos aspectos fundamentales:
- El métrico cuántico: Describe las “distancias” entre los estados cuánticos que ocupan diferentes orbitales. Esto ayuda a entender cómo responden los electrones al moverse o al interactuar con fuerzas externas.
- La curvatura de Berry: Representa un tipo de campo magnético ficticio en este espacio abstracto, que describe cómo los estados cuánticos cambian al recorrer ciertos caminos. Este concepto es clave en fenómenos topológicos, como el efecto Hall cuántico.
La importancia de la geometría cuántica radica en que determina cómo se comportan los electrones dentro de un material. Es crucial, por ejemplo, para entender por qué algunos materiales conducen electricidad sin resistencia (superconductividad) o cómo pueden diseñarse materiales con propiedades electrónicas personalizadas. Este estudio es el primero en medir directamente esta geometría en un material sólido, marcando un avance histórico en la física de materiales.

El avance: cómo lograron medir el tensor geométrico cuántico (QGT)
Para conseguir este logro, los físicos combinaron una técnica llamada espectroscopía de fotoemisión resuelta en ángulo (ARPES) con mediciones de polarización y spin. En términos sencillos, el ARPES consiste en disparar fotones hacia un material para liberar electrones, analizando luego las propiedades de estos electrones emitidos. Aunque este método se utiliza desde hace tiempo para estudiar la estructura electrónica de los materiales, los investigadores introdujeron innovaciones clave para que también pudiera medir propiedades geométricas.
Un aspecto revolucionario fue el uso de una aproximación llamada quasi-QGT, que conecta directamente los datos experimentales con las propiedades fundamentales del QGT. Este enfoque permitió reconstruir el métrico cuántico y la curvatura de Berry en materiales complejos. “El método fue concebido para ser aplicable a cualquier material genérico, independientemente de los detalles de su estructura de bandas o propiedades de simetría”, explicó Riccardo Comin. Esto significa que, además del material utilizado en este experimento, la técnica podría usarse para explorar otros sistemas, incluidos aquellos con topologías más complicadas.
El procedimiento también es notablemente eficiente, ya que requiere un conjunto mínimo de aproximaciones, lo que aumenta su robustez y aplicabilidad. Los datos obtenidos en este estudio validan las predicciones teóricas del QGT y, además, ofrecen una visión más detallada de cómo interactúan los electrones en sólidos, algo esencial para el desarrollo de nuevas tecnologías.

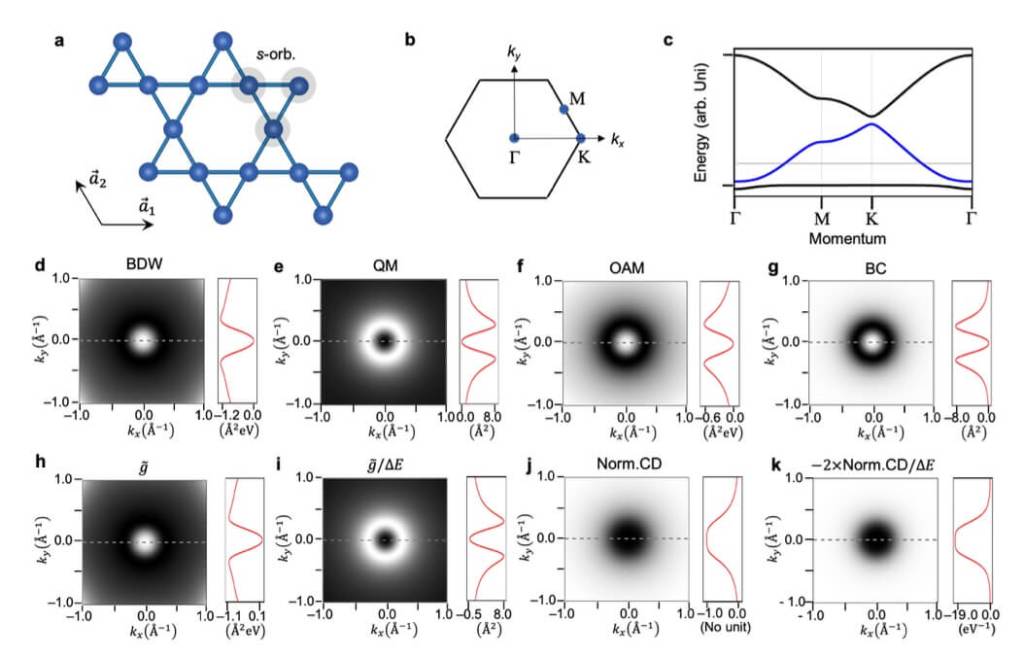
El experimento se llevó a cabo utilizando un material conocido como CoSn, un tipo de metal kagome cuya estructura cristalina es especialmente interesante para estudiar propiedades cuánticas. Los materiales kagome, que reciben su nombre de un patrón geométrico japonés, tienen una red atómica triangular con espacios vacíos, lo que genera propiedades electrónicas únicas.
En el caso de CoSn, esta estructura permite que los electrones formen bandas planas, una característica que puede conducir a fenómenos como la superconductividad o el magnetismo topológico. Usando la técnica ARPES mejorada, los investigadores lograron medir directamente la interacción entre estas bandas planas y otras bandas electrónicas llamadas bandas de Dirac, que tienen un comportamiento cuántico similar al de partículas relativistas.
Hay que tener en cuenta que la medición del QGT en este material valida el método desarrollado y demuestra cómo la geometría cuántica está intrínsecamente relacionada con las propiedades topológicas de los materiales. Los datos obtenidos revelan cómo la curvatura de Berry en CoSn influye en su capacidad para conducir electricidad sin pérdidas, lo que podría tener aplicaciones directas en la creación de superconductores más eficientes.
El CoSn es un material ideal para estos experimentos debido a su estructura simple y su estabilidad, lo que lo convierte en una plataforma modelo para explorar fenómenos cuánticos complejos.
Implicaciones futuras de este descubrimiento
Este avance puede repercutir positivamente en la física de materiales y en el diseño de nuevas tecnologías. Ahora que es posible medir directamente el QGT, los investigadores pueden estudiar cómo los electrones interactúan en una amplia variedad de materiales, incluidos aquellos con propiedades topológicas avanzadas o sistemas bidimensionales como el grafeno.
Por otra parte, la técnica desarrollada podría ayudar a descubrir materiales con superconductividad no convencional o diseñar dispositivos electrónicos más rápidos y eficientes. La capacidad de medir el QGT también conecta de manera más estrecha los experimentos con las teorías fundamentales, abriendo la posibilidad de realizar predicciones más precisas sobre el comportamiento de los materiales.
“Ahora tenemos una manera de recuperar información sobre la función de onda electrónica, y no solo sobre los niveles de energía del electrón, es decir, las bandas electrónicas”, dijo Comin. Esto podría ser la clave para desentrañar fenómenos cuánticos que hasta ahora eran imposibles de observar, revolucionando campos como la computación cuántica o la electrónica de alta velocidad.
Las aplicaciones de este avance son casi ilimitadas, y aunque aún estamos en las primeras etapas, los resultados prometen transformar nuestra comprensión de los materiales y de los fenómenos cuánticos.
Referencias
- Mingu Kang et al. Measurements of the quantum geometric tensor in solids. Nature Physics (2024). DOI: 10.1038/s41567-024-02678-8.
Cortesía de Muy Interesante
Dejanos un comentario: