¿Cuántas veces te has dejado llevar por la elegancia de los árboles? Lo cierto es que los árboles han fascinado a la humanidad desde sus orígenes, no solo por su importancia ecológica, sino también por su presencia en el arte. Desde antiguos grabados en piedra hasta las pinturas de Piet Mondrian, los árboles han sido representados de múltiples formas, pero siempre manteniendo una estructura reconocible. Ahora, un estudio reciente ha encontrado una clave matemática oculta en estas representaciones: la proporción de grosor entre las ramas.
Investigadores de la Universidad de Michigan y la Universidad de Nuevo México han analizado cómo la relación entre los diámetros de las ramas en el arte se ajusta a patrones matemáticos observados en árboles reales. Su estudio, publicado en PNAS Nexus, revela que existe un parámetro universal, denominado “exponente de escalado del diámetro de las ramas“, que permite reconocer un árbol en una imagen, incluso cuando su forma es abstracta.
Las matemáticas detrás de los árboles
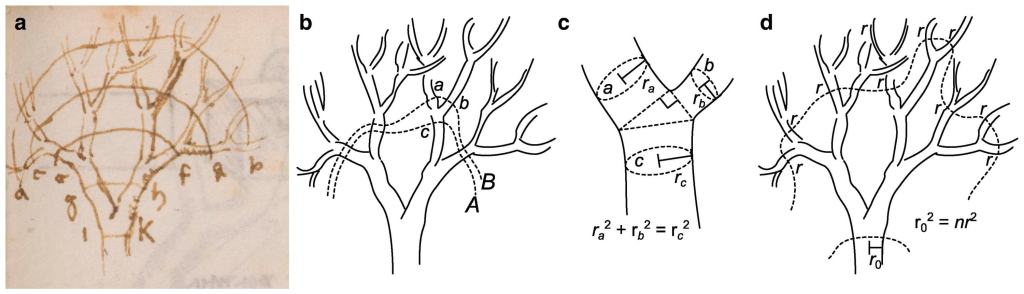
Leonardo da Vinci ya había propuesto una regla sobre el crecimiento de los árboles: el grosor total de las ramas en cada bifurcación debía ser igual al grosor del tronco. Este principio, aunque útil, no explicaba por completo la estructura fractal de los árboles. El nuevo estudio retoma esta idea y la amplía mediante el uso de la geometría fractal, una rama de las matemáticas que estudia formas que se repiten a diferentes escalas.
Los fractales aparecen en la naturaleza de muchas maneras, desde la forma de los copos de nieve hasta la estructura del sistema respiratorio humano. En los árboles, cada bifurcación repite el mismo patrón de crecimiento, pero en un tamaño reducido. Esta auto-repetición sigue un exponente de escalado, un valor matemático que regula la proporción entre ramas grandes y pequeñas. En los árboles reales, este exponente varía entre 1,5 y 3, y sorprendentemente, en el arte también.
El experimento con el arte de Mondrian
Para demostrar su hipótesis, los investigadores analizaron obras de arte de diferentes épocas y culturas, como los grabados del siglo XVI en la Mezquita Sidi Saiyyed en la India, una pintura japonesa del siglo XVIII y cuadros del pintor holandés Piet Mondrian. Este último proporcionó un caso de estudio perfecto, ya que sus obras muestran una transición desde lo figurativo hasta lo abstracto.
Mondrian pintó en 1911 El árbol gris, una imagen donde las ramas están representadas mediante líneas negras sobre un fondo gris. A pesar de su estilo simplificado, la imagen sigue siendo claramente reconocible como un árbol. El análisis matemático reveló que su exponente de escalado era 2,8, dentro del rango de los árboles reales.
Sin embargo, en 1912 Mondrian creó Árbol en flor, una obra aún más abstracta, en la que las líneas tienen un grosor uniforme. En este caso, los observadores no reconocen fácilmente la imagen como un árbol, sino que ven formas como peces, agua o bailarines. Según los investigadores, la razón es clara: el exponente de escalado desapareció.
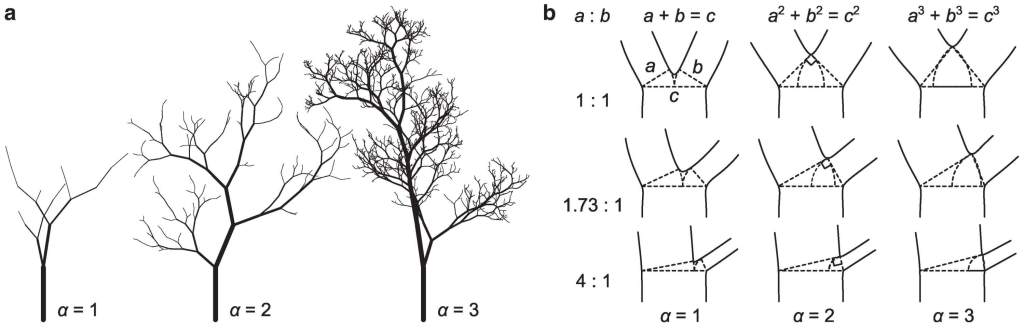
𝛼
α influye tanto en la cantidad de ramas visibles como en su proporción. A medida que
𝛼
α aumenta, los árboles generan más ramas pequeñas, creando una estructura más detallada. Además, este valor determina la relación de tamaños entre las ramas principales y secundarias, afectando la apariencia general del árbol. Fuente: PNAS Nexus
¿Por qué percibimos un árbol?
La clave de la percepción de los árboles no está solo en la forma general, sino en la relación entre los grosores de las ramas. La investigación demostró que cuando las proporciones siguen el patrón matemático natural, nuestro cerebro identifica inmediatamente la estructura como un árbol. En cambio, si esta proporción se altera o desaparece, la imagen se vuelve ambigua.
Los experimentos también analizaron cómo las diferencias culturales y estilísticas afectan esta percepción. Se observó que en las tallas en piedra de la Mezquita Sidi Saiyyed, los patrones de ramas también seguían un exponente de escalado dentro del rango de los árboles reales, a pesar de ser altamente estilizados. Esto sugiere que el cerebro humano reconoce ciertos patrones geométricos como árboles, incluso cuando no están representados de manera literal.
Las ecuaciones ocultas en los árboles: fórmulas para curiosos
Aunque los árboles parecen crecer de manera orgánica y caótica, su estructura sigue patrones matemáticos bien definidos. Leonardo da Vinci ya observó que el grosor combinado de las ramas secundarias es igual al del tronco principal. Esto se expresa con la ecuación:
Más tarde, los científicos refinaron esta idea con la geometría fractal. Se descubrió que el grosor de las ramas no siempre sigue un exponente fijo de 2, sino que puede variar entre 1,5 y 3, dependiendo de la especie del árbol y su función biológica. Así, la regla generalizada es:
Este valor α es clave para la percepción visual de los árboles, tanto en la naturaleza como en el arte. Además, el número de ramas sigue una progresión matemática: cuanto más pequeñas son, más abundantes se vuelven:
Esta relación explica por qué los árboles tienen muchas ramas delgadas en su copa, mientras que las más gruesas son menos numerosas. Lo sorprendente es que estas mismas ecuaciones se encuentran en pinturas y esculturas de diferentes épocas y culturas, guiando de manera intuitiva la representación artística de los árboles.

Más allá del arte: implicaciones científicas
Este descubrimiento no solo ayuda a entender mejor el arte, sino que también puede tener aplicaciones en biología, inteligencia artificial y diseño gráfico. En biología, el estudio refuerza la idea de que el crecimiento de los árboles sigue principios matemáticos que han sido moldeados por la evolución. En inteligencia artificial, estos hallazgos podrían mejorar los algoritmos de generación de imágenes para producir representaciones más realistas de la naturaleza.
Los investigadores también destacan la importancia de los patrones fractales en la percepción humana. La geometría fractal ya ha sido utilizada en arquitectura y diseño para crear espacios visualmente agradables, y este estudio sugiere que la misma idea podría aplicarse a la representación de árboles en medios digitales.
Referencias
Cortesía de Muy Interesante
Dejanos un comentario: