Más allá de Einstein: Introducción a las teorías de gravedad modificada claves para una futura teoría unificadora

Bien es sabido que la teoría de la Relatividad General (RG) de Einstein supuso un punto de inflexión para la física moderna a principios del siglo XX. Desde entonces, ha regalado increíbles avances tecnológicos indispensables para el día a día, como el GPS. Sin embargo, la RG contiene ciertas limitaciones en su margen teórico, es por ello que en las últimas décadas se ha intentado buscar una teoría unificadora que abarque la explicación de cualquier fenómeno físico. ¿Qué ocurre si se estudian dichas limitaciones? 

Nacen así las teorías modificadas de gravedad las cuales añaden más correcciones matemáticas de orden inferior a la teoría de Einstein. Estas teorías permiten solucionar algunos de los problemas del modelo estándar del Big Bang, ajustándose mejor a las observaciones del fondo cósmico del microondas. Por tanto, amplían el marco de la RG de Einstein para abordar sus limitaciones y representan un posible puente hacia una futura teoría unificadora, como la teoría de cuerdas o supergravedad. Debido a la complejidad de dichas teorías modificadas se va a introducir la más sencilla, la cual se denomina teoría de gravedad modificada f (R ) o de forma más resumida, teoría f (R ).

Las nuevas leyes de la gravedad: la ecuación de campo en la teoría f (R )

La ecuación de campo de Einstein es el cimiento de la RG y explica fenómenos como la gravedad, los agujeros negros y la expansión del universo. De manera sencilla: “la materia le dice al espacio-tiempo cómo curvarse, y el espacio-tiempo le dice a la materia cómo moverse”.

En analogía, la teoría f (R ) dispone de una ecuación de campo modificada también, siendo el sustrato de la misma:

Donde:

• g_ij es la métrica: describe la geometría del espacio-tiempo. 
• R_ij es el tensor de Ricci: mide la curvatura local del espacio-tiempo.
• ∇_i es la derivada covariante y □ = ∇ⁱ ∇_i es el operador d’Alembertiano.
• T_ij es el tensor energía-momento.
•  f (R ) es la nueva función que surge de la teoría modificada, depende solo del escalar de Ricci R.
• F (R ) es la derivada de f (R ) con respecto al escalar de Ricci.

¿Qué ocurre si se toma f (R ) igual a R en la ecuación anterior? En ese caso, la teoría de f (R ) reproduce exactamente la RG de Einstein. Llegando a la siguiente fascinante conclusión: la teoría de f (R ) es una extensión de la RG de Einstein; es decir, una versión más amplia que contiene a la RG como un caso particular de esta. Así, en lugar de reemplazar a Einstein, lo abarca y permite explorar nuevas posibilidades cuando la gravedad se comporta de forma diferente a lo esperado. 

Agujeros negros: la solución de Schwarzschild en f (R )

La ecuación de campo que se vio en el apartado anterior no es sencilla de resolver. De hecho, para encontrar soluciones que describan agujeros negros, deben imponerse ciertas condiciones matemáticas simplificadoras: se considera una métrica esféricamente simétrica, sin rotación, y con un escalar de Ricci constante. Además, se asume que no hay materia ni energía presentes, es decir, que el tensor energía-momento es cero: un vacío gravitacional.

En la RG, este mismo enfoque —resolver la ecuación de campo de Einstein bajo esas condiciones— lleva a una de las soluciones más famosas: la métrica de Schwarzschild. Dicha métrica fue encontrada por Karl Schwarzschild en 1915 bajo la presión de la Primera Guerra Mundial, mientras servía en el frente del este. Las condiciones inhumanas a las que estuvo sometido no fueron un impedimento para que lograra dar con la primera solución exacta a las ecuaciones de Einstein, publicada en 1916. Esta solución describe el espacio-tiempo alrededor de una masa esférica y estática, y se considera el punto de partida para entender los agujeros negros más simples.

En la teoría f (R ), si se resuelve la ecuación de campo modificada bajo las anteriores condiciones, surge una solución prácticamente idéntica a la de Schwarzschild en RG… ¡pero con un término extra! Aparece una pequeña contribución adicional que depende del escalar de Ricci, y este mismo está determinado por la función f (R ).

¿Cómo se recupera la solución clásica de la RG? Muy sencillo: basta con elegir f (R ) igual a R, de modo que el término extra resulta idénticamente nulo. Sin embargo, cuando f (R ) difiere de R, ese pequeño aporte modula por completo las propiedades del agujero negro.

Evento de sucesos: el “punto de no retorno” en agujeros negros

Una técnica eficaz para entender mejor las entidades físicas como los agujeros negros es desafiar a la propia capacidad de abstracción realizando un experimento mental: se puede imaginar el agujero negro de Schwarzschild como una esfera invisible: todo lo que cruza su superficie, llamada horizonte o evento de sucesos, desaparece irremediablemente de nuestro universo observable. Luz, materia o cualquier señal que lo atraviese queda atrapada para siempre en su interior. Mientras que fuera de ese límite podemos medir y predecir fenómenos físicos, pues dentro todo queda oculto e inaccesible.

En RG, ese horizonte se sitúa siempre a una distancia equivalente al doble de la masa del agujero negro. Pero en la teoría de gravedad modificada f (R ), la distancia de este “punto de no retorno” deja de ser un valor único y pasa a depender del escalar de Ricci R ; es decir, de la curvatura local del espacio‑tiempo… ¡Y hasta de si dicha curvatura es positiva o negativa!

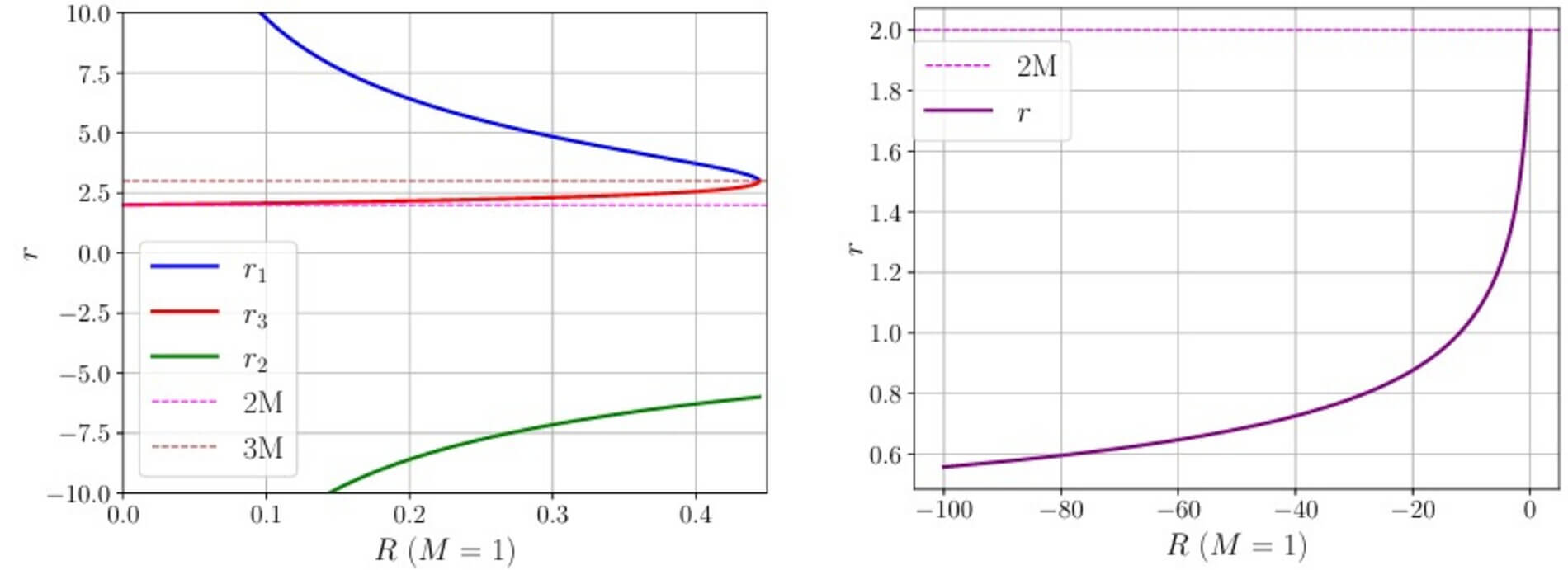
En la gráfica de la izquierda, donde se considera el escalar de Ricci positivo, aparecen tres posibles soluciones para el evento de sucesos. No obstante, solo una de ellas tiene validez física, porque si el escalar de Ricci es cero, se debe volver al resultado de RG, el de dos veces la masa. Esa solución —marcada en rojo— es la única que respeta dicho límite y, a medida que R aumenta, el horizonte de sucesos es igual a tres veces la masa del agujero negro.

Por otro lado, cuando R es negativo (gráfica de la derecha) surge una única solución real para el horizonte de sucesos, adaptándose perfectamente al caso de la RG cuando la curvatura tiende a cero.

ISCO: El último baile estable alrededor del agujero negro

Ya se conoce cómo nace un agujero negro a partir de la solución descrita por Schwarzschild, así como su principal característica: el horizonte de sucesos. Pero ¿qué sucede si se coloca una partícula con masa en el entorno de un agujero negro? La respuesta está en el delicado equilibrio entre la atracción gravitatoria y la fuerza centrífuga que experimenta al moverse en torno al agujero negro.

Para ilustrarlo, basta imaginar el posible “camino” que describiría la partícula: desde órbitas circulares amplias, donde la velocidad de giro compensa la atracción, hasta trayectorias en forma de espirales que la arrastran inevitablemente hacia el misterioso interior. Sin embargo, existe un límite muy preciso: la ISCO —Innermost Stable Circular Orbit— u “Órbita Circular Estable más Interna”. En RG, este radio crítico se sitúa en seis veces la masa del agujero negro. Para distancias menores, ya no hay forma de mantener un equilibrio estable: cualquier pequeña perturbación precipita a la partícula hacia el horizonte de sucesos.

Pero la RG no es la última palabra. Estudiando la teoría de gravedad modificada f (R ) uno podría llegar a preguntarse: ¿Cómo se comporta la ISCO en esta teoría? Se trata de una trayectoria compleja que, al igual que ocurría con el evento de sucesos, depende del escalar de Ricci, así como de su signo. 

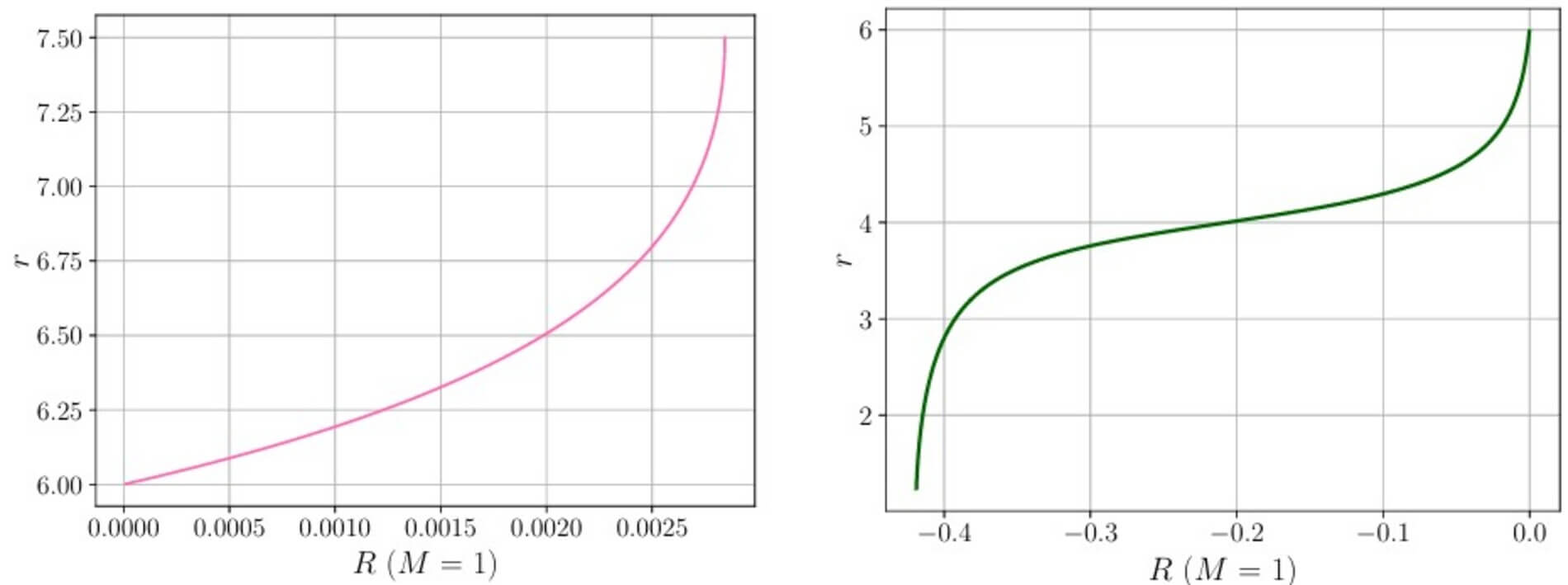
Se aprecia que ambas gráficas cumplen el límite de RG, es decir, si R es cero, la ISCO se sitúa en seis veces la masa del agujero negro. Además, si el escalar de Ricci es positivo — gráfica de la izquierda — la ISCO alcanza su máximo en 7.5 veces la masa del agujero negro.

Potencial efectivo: el equilibrio entre “tirón” gravitatorio y “empuje” centrífugo

Para entender por qué la ISCO marca el último baile circular, hay que analizar el potencial efectivo, que combina en una sola curva:

• El “tirón” gravitatorio, que atrae la partícula hacia el agujero negro.
• El “empuje” centrífugo, que tiende a mantenerla alejada.

Al representarlo gráficamente frente a la distancia, aparece un máximo (órbita inestable) seguido de un mínimo (órbita estable). El punto de inflexión que marca la frontera entre el mínimo y el máximo es precisamente la ISCO.

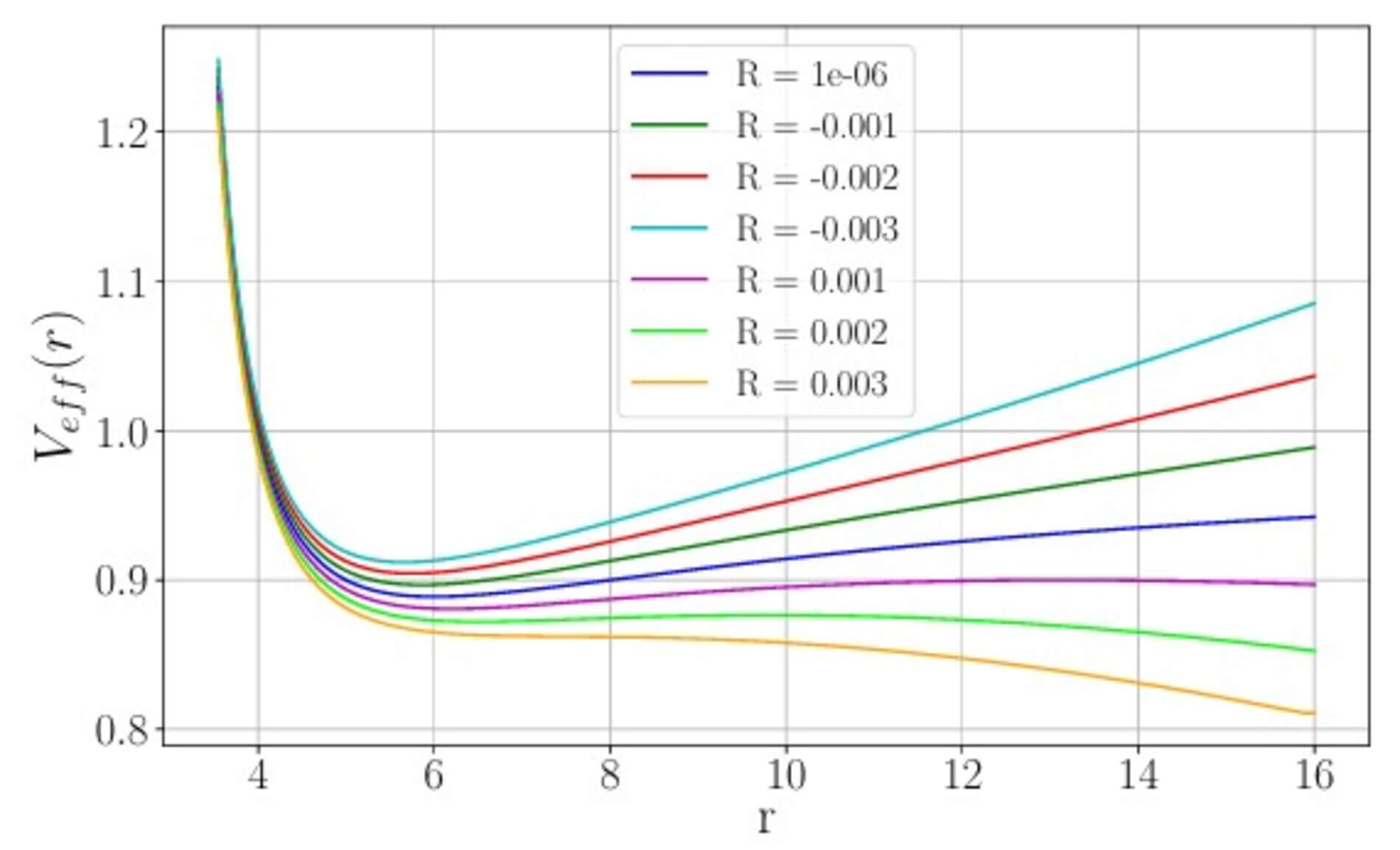
Al representar el potencial efectivo en función de la distancia para diferentes valores del escalar de Ricci se aprecia que:

• Para R < 0 el mínimo local persiste, pero se estrecha, confinando las órbitas estables a un rango de distancias menor.
• Para R > 0, si es suficientemente grande, el mínimo desaparece por completo, convirtiéndose en un único punto de inflexión sin “valle” estable.

En consecuencia, un escalar de Ricci positivo demasiado grande borra el oasis de estabilidad donde la fuerza centrífuga compensa la atracción gravitatoria. Por tanto, para garantizar órbitas circulares estables, R debe mantenerse por debajo de un umbral que conserve ese mínimo en el potencial efectivo.

Desafío a Kepler: pequeñas correcciones en su famosa fórmula

La tercera ley de Kepler establece que la frecuencia angular orbital al cuadrado es inversamente proporcional al cubo de la distancia al cuerpo central. Durante siglos, esta ley ha imperado sobre el movimiento planetario, marcando un orden perfecto.

En el marco de la RG, con la métrica de Schwarzschild, dicha proporción se recupera de forma exacta, incluso en regiones de gravedad intensa, reforzando la confianza en las predicciones de Einstein.

¡Pero la teoría de gravedad modificada f (R ) plantea un giro inesperado! Al introducir una dependencia más compleja de la curvatura del espacio‑tiempo, aparece un segundo término, pequeño, pero no despreciable, que provoca una desviación sutil de la relación kepleriana. 

¿Por qué importan las teorías de gravedad modificada?

La familia de teorías de gravedad modificada busca ir más allá de la RG. Dentro de estas teorías, la de f (R ) destaca por su simplicidad. Se ha obtenido la solución tipo Schwarzschild y sus propiedades más importantes — el horizonte de sucesos, el radio del ISCO y el potencial efectivo para partículas masivas— que desnudan matices inéditos en la física de agujeros negros.

¿No sorprende que hasta una ley tan consagrada como la tercera ley de Kepler muestre una pequeña desviación en estas teorías? ¡Ese “segundo término” que añade, f (R ) convierte a la ley kepleriana en una aproximación, y su violación leve se convierte en una oportunidad para experimentos de gran precisión! Así,  f (R ) y el conjunto de teorías modificadas no solo refuerzan nuestro entendimiento de la gravedad, sino que ofrecen predicciones nuevas y medibles que podrían desvelar secretos más profundos de la naturaleza.

En definitiva, el valor de las teorías de gravedad modificada radica en su capacidad para extender el legado de Einstein, conservando sus aciertos y a la vez abriendo puertas a posibles explicaciones de misterios de los fenómenos físicos. Gracias a estos modelos, la física teórica y la observación se aúnan para poner a prueba los límites de la gravedad.

Cortesía de Muy Interesante

Dejanos un comentario: