A comienzos del siglo XX, el físico británico Horace Lamb propuso un modelo para describir el comportamiento de una partícula vibrante en un medio elástico. El problema era bien conocido en la física clásica: al vibrar, la partícula genera ondas que se propagan por el medio y, a su vez, disipan la energía del sistema. Sin embargo, cuando se quiso traducir este fenómeno al lenguaje cuántico, surgieron obstáculos que se prolongaron… hasta hoy. Un siglo más tarde, un estudiante universitario y su mentor han conseguido resolver este enigma en el contexto de la física cuántica. El terreno de los osciladores cuánticos está sembrado de posibilidades futuras.
Nam H. Dinh, junto con su profesor Dennis P. Clougherty, ha dado con una solución exacta al llamado modelo cuántico de Lamb, que describe el comportamiento de un oscilador armónico amortiguado a escala atómica. El hallazgo, publicado en Physical Review Research, ha resuelto un problema planteado en 1900 con herramientas modernas de mecánica cuántica. Lo llamativo es que uno de los autores aún era estudiante de máster al presentar el trabajo. Su contribución ha sido crucial para abordar un modelo que, hasta ahora, había resistido todo intento de solución rigurosa en el ámbito cuántico.
Del modelo clásico a la versión cuántica
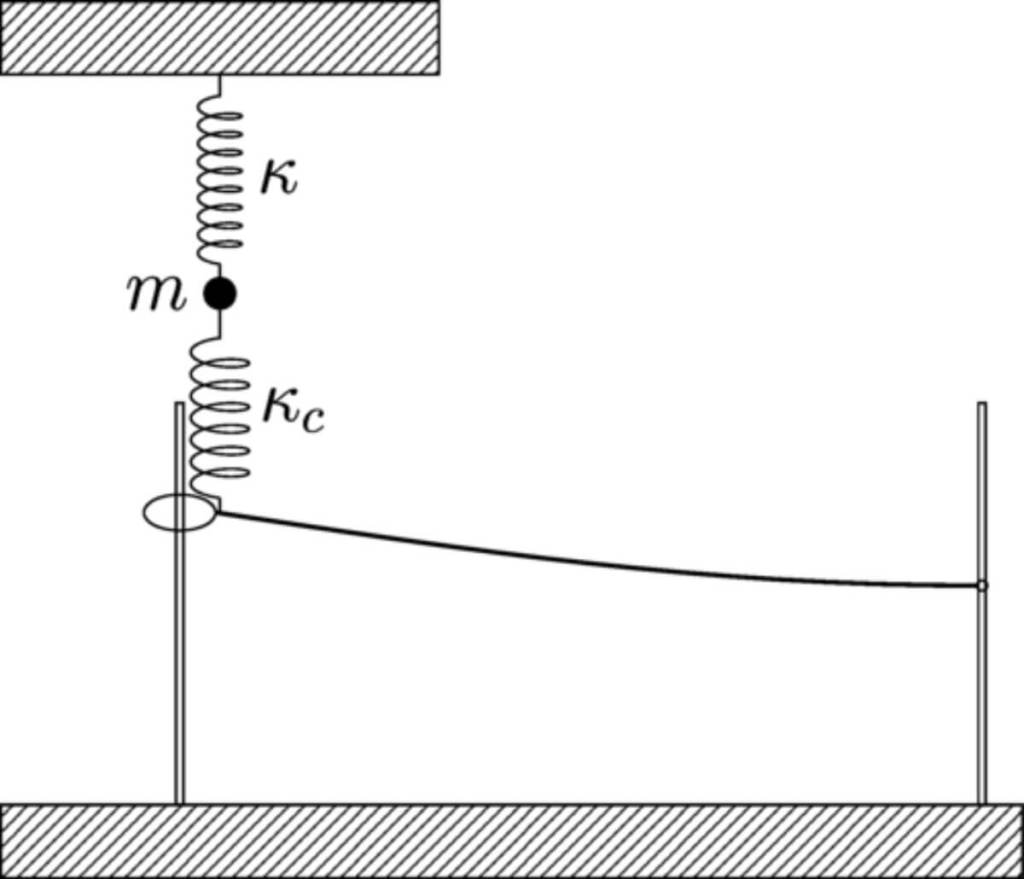
El modelo original propuesto por Lamb describía cómo una partícula vibrante pierde energía al generar ondas en un medio continuo. Esa pérdida de energía —amortiguamiento— podía explicarse con las leyes de Newton y se consideraba resuelto en el marco clásico. Pero cuando los físicos intentaron trasladar esa misma idea al mundo atómico, surgieron conflictos fundamentales con los principios de la mecánica cuántica.
Uno de los mayores desafíos era compatibilizar el comportamiento disipativo del sistema con el principio de incertidumbre de Heisenberg, que impone límites estrictos a la precisión con que se pueden conocer simultáneamente la posición y el momento de una partícula. Incluir la pérdida de energía en un sistema cuántico sin violar este principio fue, durante décadas, un obstáculo insalvable.
Dinh y Clougherty reformularon el modelo de Lamb adaptándolo al contexto cuántico, pero sin simplificaciones que lo alejaran de su riqueza física. Su propuesta mantiene la estructura original del sistema, dividido en una partícula vibrante (el oscilador) y un medio que actúa como entorno (la cuerda), pero incorpora formalmente el acoplamiento entre ambos elementos en forma de operadores bilineales. Esta formulación permitió aplicar una transformación matemática conocida como transformación de Bogoliubov, con la que se pudo resolver el sistema de forma exacta.
Una solución exacta tras 125 años
El principal logro de este trabajo es haber encontrado una solución exacta para un sistema físico que, hasta ahora, solo podía abordarse con aproximaciones. El artículo señala que “el modelo proporciona un ejemplo resoluble del oscilador armónico cuántico amortiguado”. Esto quiere decir que no se trata de una simulación ni de una solución parcial. Es decir, el sistema ha sido descrito matemáticamente en toda su complejidad, respetando las reglas de la mecánica cuántica.
Además, los autores calcularon la frecuencia de oscilación del sistema y la tasa de amortiguamiento mediante una ecuación integral no lineal, lo que les permitió describir también el estado base del sistema. Este estado, lejos de ser simple, es un vacío comprimido multimodal, una configuración cuántica en la que se reduce la incertidumbre en la posición de la partícula a costa de aumentar la del momento.
Esta idea de redistribuir la incertidumbre se ha utilizado antes en física para mejorar la precisión en las mediciones, como en los detectores de ondas gravitacionales. Pero ahora, gracias al trabajo de Clougherty y Dinh, se demuestra que este tipo de estados pueden emerger de manera natural en sistemas físicos concretos.
El estado base obtenido es, según el artículo, “siempre un estado de vacío comprimido multimodal”, lo que confirma que la naturaleza cuántica del sistema queda reflejada incluso en su configuración más estable. A partir de esta base, los investigadores calcularon también el espectro de excitaciones y la forma en que se propaga la energía a través del sistema.
Vacío comprimido multimodal: un estado cuántico peculiar, pero clave
El llamado vacío comprimido multimodal es el estado base del sistema descrito por Clougherty y Dinh. Se trata de una forma especial del vacío cuántico —el estado de menor energía posible— en el que se ha aplicado un proceso matemático llamado compresión cuántica (squeezing). Esto permite reducir la incertidumbre en una propiedad concreta del sistema (como la posición), a costa de aumentarla en otra (como el momento), siempre respetando el principio de incertidumbre de Heisenberg. La novedad es que esta compresión no ocurre sobre un solo modo de vibración, sino de forma simultánea sobre muchos modos distintos del sistema, lo que le da el carácter de “multimodal”.
Este tipo de estados ya se conocía en óptica cuántica y en teoría cuántica de campos, pero su aparición como solución exacta y natural en un sistema físico concreto, como ocurre en este modelo, no es habitual. El vacío comprimido multimodal refleja de forma precisa cómo interactúan la partícula vibrante y su entorno, y permite calcular propiedades esenciales como la tasa de disipación o la distribución de excitaciones. Lejos de ser una construcción abstracta, este estado tiene aplicaciones prácticas en áreas donde se requiere medir con extrema precisión, como en detectores de ondas gravitacionales o tecnologías de sensores cuánticos.

El papel clave de un joven investigador
Nam H. Dinh era estudiante de máster cuando contribuyó a este avance. Tras graduarse en física en la Universidad de Vermont en 2024, trabajó con Clougherty en este modelo durante su posgrado y actualmente realiza su doctorado en matemáticas. Su rol no fue el de un colaborador menor: su participación permitió derivar y resolver las ecuaciones que otros autores habían evitado por su complejidad.
La colaboración entre ambos autores permitió aprovechar tanto la experiencia de Clougherty como la versatilidad matemática de Dinh. El trabajo no es solo una demostración técnica, sino un ejemplo de cómo el talento joven puede marcar una diferencia real en investigación básica. En lugar de simplificar el sistema o acudir a métodos puramente numéricos, lograron mantener la estructura analítica del modelo hasta el final.
“En la física clásica, se sabe que cuando los objetos vibran u oscilan, pierden energía debido a la fricción, la resistencia del aire, etc.”, declara Dinh. “Pero esto no es tan obvio en el régimen cuántico”, añade.

Relevancia práctica y futuras aplicaciones
Aunque el trabajo es teórico, sus implicaciones prácticas son claras. Una de ellas es la posibilidad de diseñar sensores cuánticos más precisos, capaces de medir distancias o variaciones extremadamente pequeñas. Esto se debe a que, al reducir la incertidumbre en la posición, se pueden hacer mediciones por debajo del límite cuántico estándar.
El modelo predice cómo varía la incertidumbre en función del acoplamiento entre la partícula y el entorno, y permite calcular de forma exacta la tasa de disipación de energía. Esta información puede ser útil para entender sistemas reales, como átomos en sólidos, vibraciones en nanoestructuras o circuitos cuánticos que necesitan minimizar la pérdida de coherencia.
También se abre la puerta a estudiar otros sistemas físicos con una estructura parecida. Los autores mencionan que sus resultados podrían aplicarse a “una variedad de sistemas cuánticos relacionados”, como modos vibracionales en aislantes magnéticos o cavidades electromagnéticas. Esto convierte al modelo cuántico de Lamb en una herramienta de referencia para explorar nuevas configuraciones físicas.
El logro no solo es una victoria para la física teórica, sino también una posible fuente de inspiración para diseñar experimentos que verifiquen estas predicciones. La precisión alcanzada por el modelo hace posible que se puedan contrastar sus resultados con datos experimentales en plataformas como sistemas optomecánicos o resonadores cuánticos.
Referencias
Cortesía de Muy Interesante
Dejanos un comentario:

