El comportamiento de los gatos enamora a la humanidad desde hace siglos, unos animales famosos tanto por su independencia como por su enigmático carácter. A pesar de su popularidad, los mecanismos físicos detrás de sus actitudes no se han estudiado lo suficiente, y cada intento por explicarlo despierta gran interés en la comunidad científica. Recientemente, el físico gallego Anxo Biasi ha logrado algo extraordinario al proponer un modelo matemático para describir el movimiento de los gatos en presencia de humanos. Se trata una perspectiva original que está basada en las leyes de la física clásica.
En un artículo publicado en la American Journal of Physics, Biasi presenta una ecuación de movimiento que describe comportamientos típicos de los gatos, como su tendencia a mantener cierta distancia de las personas, el fenómeno del “zoomies” (esos momentos de carrera frenética por la casa), y el “purring” (ronroneo). Según el autor, este modelo no solo reproduce estos patrones de interacción entre gatos y humanos, sino que también ofrece una herramienta para la enseñanza de conceptos básicos de mecánica.
Modelando al gato como una partícula puntual
Biasi ha desarrollado su investigación modelando al gato como una “partícula puntual” en movimiento bajo la influencia de una persona estática. Este enfoque simplificado permite analizar el comportamiento del animal sin la necesidad de representaciones complejas. En este modelo, la persona genera un “potencial” de atracción o repulsión que influye en el gato, donde factores como la “fricción” y el “acoplamiento” del gato hacia la persona juegan un papel fundamental.
Para explicar por qué los gatos suelen mantener cierta distancia de los humanos, el modelo incluye un potencial con “mínimos” fuera del centro, lo cual genera una preferencia de reposo para el gato en ciertos puntos específicos. Biasi utiliza el concepto de fricción para describir cómo el gato se desplaza hacia estos puntos de equilibrio después de períodos de actividad. Así, el modelo permite observar patrones de comportamiento que reflejan la tendencia del gato a evitar el contacto directo y buscar ubicarse a una distancia segura de las personas.
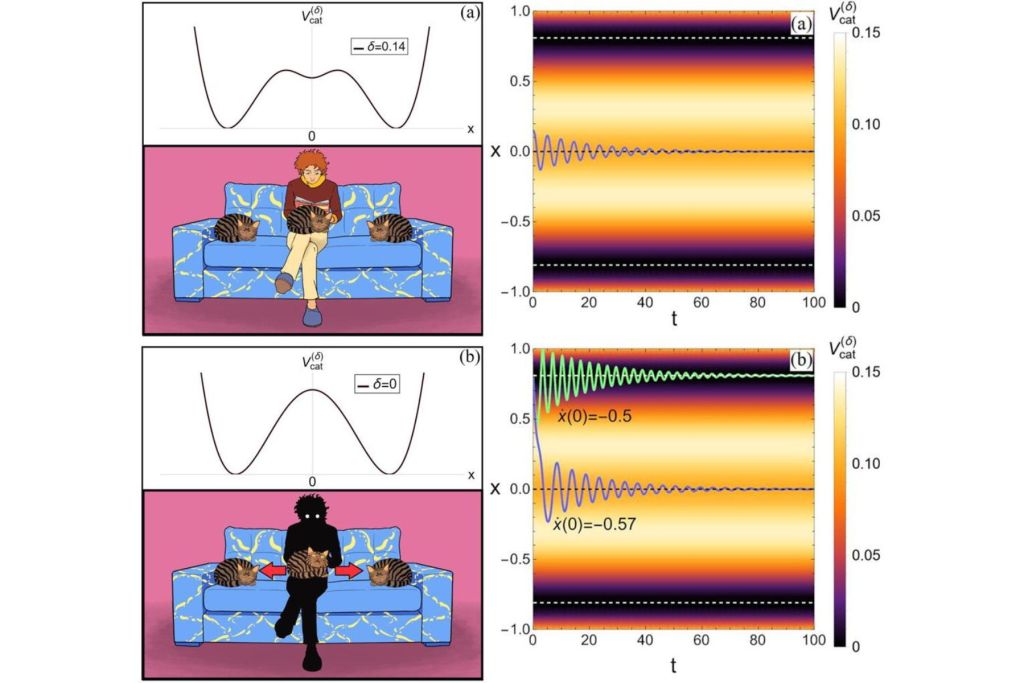
La ecuación de movimiento y el vínculo con el comportamiento felino
La ecuación que propone Biasi adopta la forma de una ecuación diferencial clásica que a cualquier físico le parecería familiar, en la que el gato se ve influido tanto por la fricción como por el potencial de la persona. Este potencial varía según el “grado de apego” del gato hacia el humano, de modo que, a mayor apego, mayor es la tendencia del gato a quedarse cerca de la persona.
La ecuación de movimiento también explica por qué los gatos a veces se comportan de forma “caprichosa” cuando los llaman, pero no siempre responden. Según el modelo, la atracción hacia el humano depende de la energía aplicada en el llamado; es decir, si la llamada no genera suficiente impulso, el gato no supera la barrera de potencial que lo retiene en su zona de comodidad. En este sentido, la ecuación refleja una percepción “física” del gato, que responde al estímulo solo si este es lo bastante fuerte para motivarlo.

Comportamientos observados: de la indiferencia a las “zoomies”
Biasi identifica varios comportamientos específicos que la ecuación es capaz de modelar, como la indiferencia al llamado y las “zoomies” nocturnas. Estas últimas, caracterizadas por correr de un lado a otro en un aparente estado de euforia, son explicadas en el artículo mediante la inclusión de un término estocástico o aleatorio en la ecuación de movimiento. Este término simula impulsos de energía que empujan al gato a cambiar de posición de manera impredecible, fenómeno común en gatos jóvenes, quienes tienen menor fricción y mayor energía.
Las “zoomies” se describen como un “proceso estocástico” donde el movimiento del gato se vuelve caótico e impredecible, de forma similar al movimiento browniano en partículas suspendidas en un líquido. Este fenómeno se observa más en gatos jóvenes y enérgicos, mientras que en gatos mayores, donde la fricción es mayor, la actividad se ve naturalmente limitada.

El ronroneo como un mecanismo de estabilización
Otro comportamiento felino abordado en el estudio es el ronroneo. Biasi sugiere que este característico sonido podría actuar como un mecanismo de estabilización. Basándose en el concepto del “péndulo de Kapitza”, el ronroneo se modela como una fuerza vibratoria externa que refuerza la relación de estabilidad entre el gato y el humano. Según el artículo, esta vibración podría actuar como una fuerza estabilizadora, permitiendo que el gato permanezca cerca de la persona sin moverse. El péndulo de Kapitza es un sistema en el que un péndulo invertido puede mantenerse estable si se le aplica una vibración rápida en su punto de suspensión.
Este mecanismo resulta particularmente interesante porque también explica por qué el gato es propenso a quedarse en el regazo de una persona mientras ronronea. La vibración inducida actúa como una “fuerza de sujeción” adicional, manteniendo el equilibrio y creando una estabilidad que permite al gato permanecer en su posición preferida por más tiempo. Esta teoría abre nuevas vías para indagar cómo la física puede explicar comportamientos animales complejos.

Aplicaciones pedagógicas del modelo
Más allá de la fascinación por entender a los gatos, el modelo de Biasi tiene también implicaciones pedagógicas. Al tratarse de una aplicación de la física clásica en situaciones cotidianas, proporciona una herramienta accesible para enseñar conceptos de mecánica como puntos de equilibrio, barreras de potencial y fricción. Según el autor, el uso de gatos en lugar de objetos inanimados podría mejorar la comprensión de los estudiantes al representar un ejemplo “menos abstracto” de la física.
El enfoque de Biasi demuestra cómo la física puede aplicarse en áreas inesperadas, facilitando la enseñanza mediante ejemplos atractivos. Este tipo de modelos pueden emplearse en clases de física introductoria, donde los estudiantes suelen encontrar dificultades para visualizar conceptos teóricos en sistemas abstractos. En palabras del autor, el modelo ayuda a “asimilar conceptos mientras se observa que la física puede ser usada de una forma divertida y estimulante”.
Referencias
Cortesía de Muy Interesante
Dejanos un comentario: