Puede que no sea el primer deporte que viene a la mente cuando hablamos de física aplicada, pero los bolos han despertado un inesperado interés científico. Esta afición que mezcla ocio, precisión y estrategia tiene más de 45 millones de practicantes anuales en Estados Unidos, y también está creciendo en España, con nuevas ligas, espacios recreativos y un perfil de jugador cada vez más diverso. La cuestión no es ya solo derribar todos los bolos, sino entender por qué algunos tiros, aparentemente idénticos, terminan en éxito o fracaso. Hace poco hablábamos del teorema de la bola peluda, en este caso no tiene pelos, pero sí agujeros.
En ese contexto, un equipo internacional de investigadores de Princeton, el MIT, la Universidad de Nuevo México, Loughborough y Swarthmore ha desarrollado un modelo físico detallado que permite predecir la trayectoria de una bola de bolos. La investigación, publicada en la revista AIP Advances, parte de un enfoque poco habitual en este ámbito: modelar matemáticamente el tiro perfecto utilizando ecuaciones diferenciales basadas en la rotación de un cuerpo rígido, concretamente a partir de las ecuaciones de Euler. El objetivo: saber con precisión cuál es la mejor forma de lanzar para conseguir un strike.
El desafío de simular una bola de bolos en movimiento
La trayectoria de una bola de bolos no es tan sencilla como parece. Aunque la escena es familiar —una bola pesada deslizándose por una pista encerada hacia un conjunto de diez bolos—, la cantidad de factores físicos en juego es sorprendente. El peso (masa, en realidad) y la forma interna de la bola, la rotación impartida por el jugador, la fricción del suelo, el ángulo de lanzamiento, la distribución del aceite sobre la pista… todo influye en el resultado.
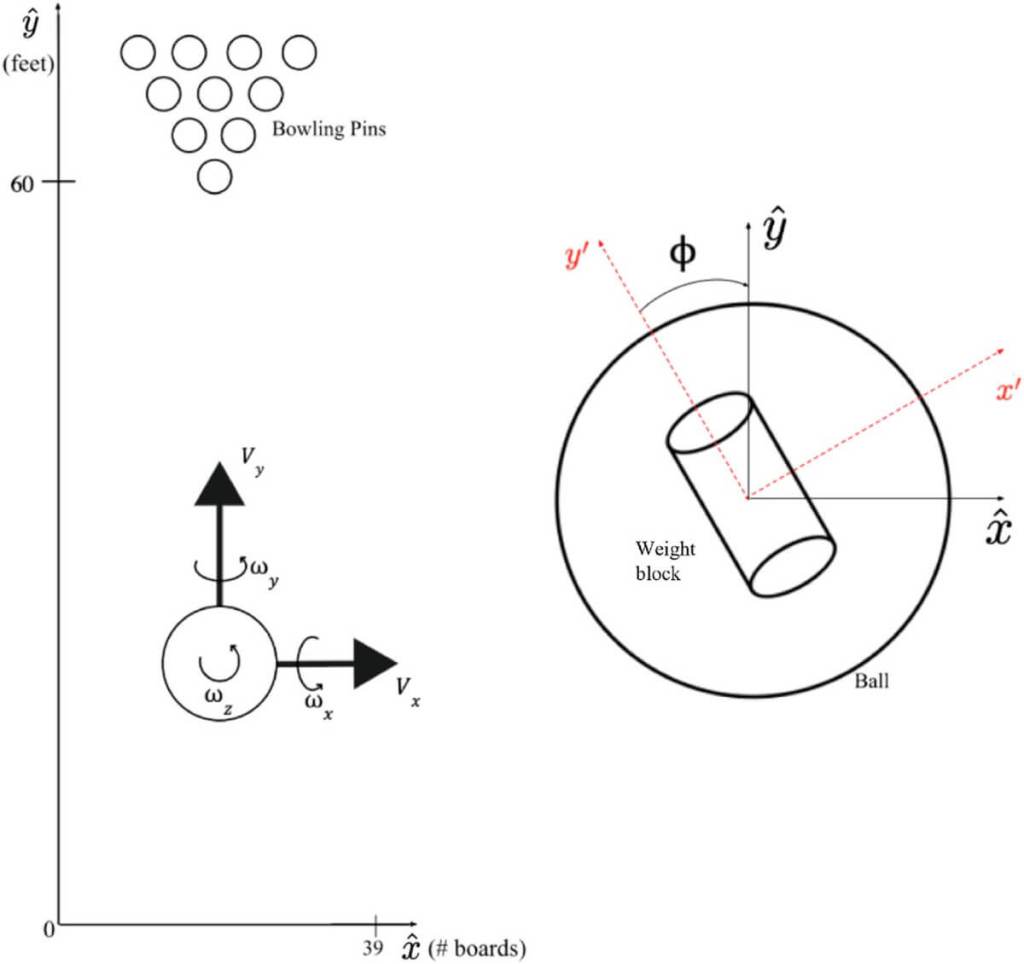
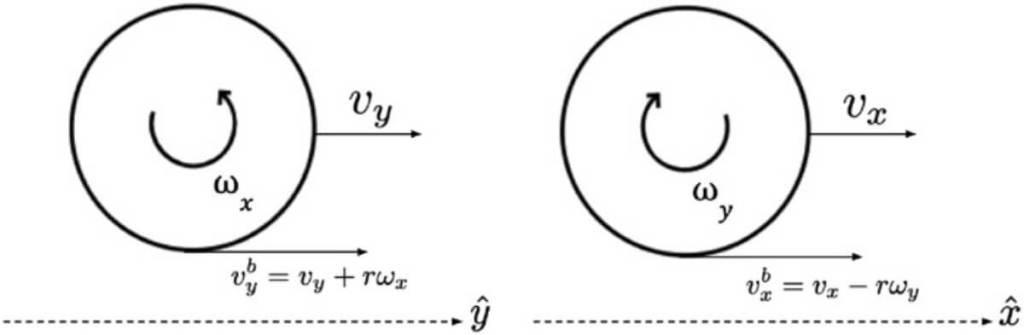
El modelo desarrollado por el equipo de investigación utiliza un sistema de seis ecuaciones diferenciales acopladas, que describen cómo evoluciona el movimiento de la bola desde el momento en que se suelta hasta que impacta con los bolos. Este enfoque matemático parte de las ecuaciones de Euler para un cuerpo rígido en rotación, un marco clásico de la mecánica que permite calcular cómo interactúan las distintas fuerzas implicadas. Según el artículo, “las ecuaciones de movimiento descritas en esta sección representan la rotación de un cuerpo rígido utilizando un marco de referencia en rotación fijado a la bola”.
Uno de los mayores retos fue adaptar estas ecuaciones a una bola de bolos real, que no es perfectamente simétrica. Muchas bolas de competición tienen un “bloque de peso” interno que altera el centro de masas y cambia su comportamiento durante el giro. Para simplificar los cálculos, los autores asumieron que el centro de gravedad está centrado, aunque reconocen que futuras versiones del modelo podrían incorporar esta complejidad.

Aceite, fricción y precisión: variables clave del modelo
Una de las grandes novedades del estudio es que el modelo tiene en cuenta la distribución de aceite sobre la pista, un detalle fundamental en competiciones profesionales. Este aceite se aplica en patrones específicos para modificar la fricción y hacer más difícil predecir la trayectoria de la bola. Como explican los autores, “los patrones de aceite en competición están diseñados específicamente para crear perfiles de fricción que varían y que dejan márgenes de error diferentes”.
Esto se traduce en que dos tiros iguales, lanzados en diferentes zonas de la pista, pueden comportarse de forma completamente distinta. Por eso, el modelo no solo simula la trayectoria ideal, sino que también calcula un “margen de error”, lo que llaman miss-room, para representar las pequeñas imprecisiones humanas. Los jugadores no son máquinas, y el modelo considera que incluso los mejores profesionales pueden desviarse unos grados respecto al ángulo de lanzamiento ideal. Esta variación se introduce mediante una distribución gaussiana, con una desviación estándar de 0,1 grados.
Los resultados son útiles no solo para entender qué zona de la pista es más favorable para lanzar, sino también para diseñar estrategias personalizadas según el tipo de bola, el estilo del jugador y el patrón de aceite aplicado. Como reconocen los autores, “al incorporar un margen de error humano, el modelo permite a los jugadores encontrar su propia estrategia de puntería óptima”.
¿Cómo se determina la mejor estrategia?
El estudio se centra en encontrar el mejor punto de partida y el ángulo de lanzamiento óptimo para maximizar la probabilidad de conseguir un strike. Para ello, se simularon miles de combinaciones posibles de posición inicial y ángulo de lanzamiento, en dos tipos de patrones de aceite: uno uniforme (“flat”) y otro corto, más complejo.
En el caso del patrón uniforme, los resultados muestran que no hay una gran diferencia entre varias combinaciones de lanzamiento. Sin embargo, con el patrón corto, se observa una “línea ideal” muy clara: una zona de la pista que proporciona la mayor probabilidad de éxito incluso si el jugador se desvía ligeramente. Esto es especialmente útil para jugadores intermedios, que no siempre repiten el mismo tiro con exactitud.
No se trata solo de tirar fuerte o de tener suerte: hay ciencia detrás de cada curva, cada giro y cada impacto
Según el estudio, “la línea ideal forma una trayectoria que se alinea estrechamente con el límite entre dos zonas de fricción del patrón de aceite corto”. Esto tiene una explicación física: si la bola se lanza ligeramente hacia la derecha, la fricción más alta cerca del canal la hace girar hacia la izquierda; si se lanza un poco a la izquierda, la fricción más baja en el centro permite que se mantenga en su curso. El resultado es una zona más tolerante a los errores, lo que aumenta significativamente las probabilidades de un strike.
Además, esta simulación puede ser especialmente útil para entrenadores y diseñadores de competiciones, ya que permite anticipar qué tan fácil o difícil será conseguir buenos resultados con un determinado patrón de aceite. Se convierte, así, en una herramienta tanto analítica como práctica para la preparación de torneos.
Aplicaciones prácticas y perspectivas de futuro
Este tipo de modelo tiene aplicaciones claras en el ámbito competitivo, pero también puede resultar útil para jugadores amateur que quieran mejorar su rendimiento. El software desarrollado podría, en teoría, ajustarse a los datos individuales de cada jugador —velocidad, rotación, inclinación del eje, tipo de bola— para generar una estrategia personalizada que maximice las opciones de éxito.
El estudio también abre la puerta a investigaciones más amplias. Por ejemplo, se podrían incorporar otras variables que actualmente no se tienen en cuenta, como la topografía de la pista o el tipo de material del suelo, que pueden influir en la fricción real. También podría mejorarse la representación del contacto entre bola y pista, que en este modelo se simplifica como un punto único.
Además, el modelo puede ayudar a los jugadores a seleccionar mejor su equipamiento. Dado que cada bola tiene características propias —peso, distribución interna, tipo de superficie—, saber cuál se comporta mejor en un determinado patrón de aceite puede marcar la diferencia en una competición.
Aunque los investigadores reconocen que “se requiere trabajo experimental adicional para proporcionar un conjunto más preciso de coeficientes de fricción”, los resultados actuales ya representan un avance importante frente a los métodos empíricos tradicionales, que se basaban en observar estadísticas sin entrar en la física real del movimiento.
En definitiva, este estudio demuestra que incluso una actividad tan cotidiana como jugar a los bolos puede beneficiarse del análisis riguroso de la física y las matemáticas. No se trata solo de tirar fuerte o de tener suerte: hay ciencia detrás de cada curva, cada giro y cada impacto.
Referencias
- S. S. M. Ji, S. Yang, W. Dominguez, C. G. Hooper, C. S. Bester. Using physics simulations to find targeting strategies in competitive tenpin bowling. AIP Advances 15, 045222 (2025). https://doi.org/10.1063/5.0247761
Cortesía de Muy Interesante
Dejanos un comentario: