Las creencias no son fijas. Se ajustan con la experiencia. Si alguien se hace una prueba médica y ya se sentía enfermo, no interpretará igual un resultado positivo que si estaba perfectamente. Eso, que parece sentido común, tiene una base matemática: la regla de Bayes. Esta herramienta estadística, con más de 250 años de historia, sirve para actualizar nuestras probabilidades cuando llega nueva información.
Ahora, un equipo internacional de investigadores ha llevado esta regla al terreno de la física cuántica. Lo han conseguido a través de un principio fundamental: el de cambio mínimo. Su propuesta da lugar a una versión cuántica de la regla de Bayes, con aplicaciones posibles en computación, aprendizaje automático y más. El estudio se ha publicado en la revista Physical Review Letters y ofrece una reformulación que respeta las particularidades del mundo cuántico, donde la lógica clásica no siempre se cumple.
De la probabilidad clásica a la cuántica
La regla de Bayes se formuló en 1763 y permite ajustar la probabilidad de un evento teniendo en cuenta información previa. En el mundo clásico, esta regla es ampliamente usada en medicina, inteligencia artificial, meteorología o finanzas. Sirve, por ejemplo, para saber cuán probable es que una persona tenga gripe si ha dado positivo en un test, pero también si ya presentaba síntomas antes.
El artículo parte de una idea simple pero poderosa: “la regla de Bayes puede derivarse de un principio de cambio mínimo”. Es decir, al recibir nueva información, deberíamos modificar lo mínimo posible nuestras creencias previas, siempre que estas sigan siendo coherentes con los nuevos datos. Este principio busca mantener la consistencia sin exagerar el ajuste.
El reto era trasladar esa idea al mundo cuántico, donde las probabilidades no se comportan de forma intuitiva. En la física cuántica, no hablamos de certezas sino de estados que representan probabilidades superpuestas. Una partícula no tiene una posición concreta hasta que se mide. Antes de eso, solo hay una distribución de posibilidades.
Fidelidad cuántica: cómo medir el cambio
Para adaptar la regla de Bayes al entorno cuántico, los autores del estudio emplean un concepto central en teoría cuántica: la fidelidad. Esta mide cuán parecidos son dos estados cuánticos. Si la fidelidad es alta, significa que hay poco cambio entre un estado inicial y uno actualizado.
Lo que hacen los investigadores es aplicar un método de optimización que busca “maximizar la fidelidad entre el proceso directo y el inverso”. En otras palabras, tratan de ajustar un estado cuántico tras recibir nueva información, pero cambiándolo lo menos posible. Esta idea refleja fielmente el espíritu de la regla de Bayes en su versión clásica.
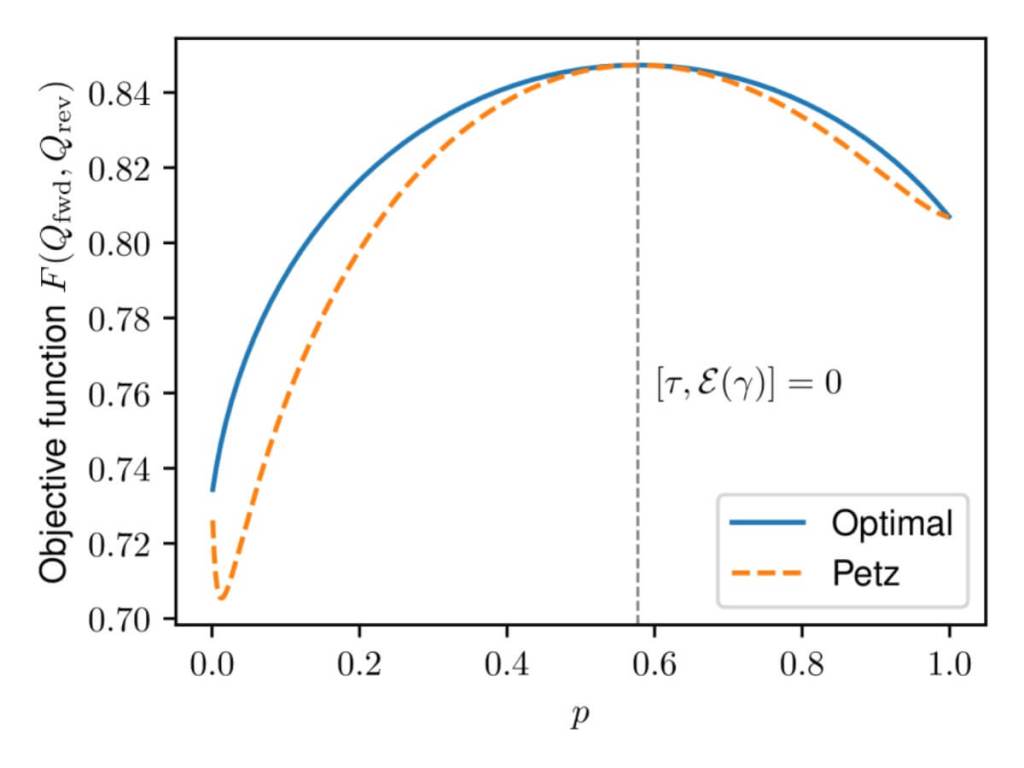
El resultado es una formulación de la regla de Bayes en clave cuántica que no solo es coherente, sino que además coincide en muchos casos con una propuesta previa: el llamado mapa de Petz. Este mapa ya era conocido, pero no se había derivado a partir de un principio general. Ahora, sí.
El mapa de Petz y la validación matemática
El mapa de Petz es una fórmula que se usa en física cuántica para recuperar información perdida. Durante años se sospechaba que podía ser una buena versión cuántica de la regla de Bayes, pero hasta ahora no se había demostrado desde un principio de mínimos.
En el artículo, los autores demuestran que cuando se cumplen ciertas condiciones, como que los estados de entrada y salida sean compatibles (conmutativos), “la solución coincide con el mapa de Petz con respecto al canal y al estado inicial”. Este hallazgo refuerza la validez de dicha herramienta en contextos como la corrección de errores en computación cuántica.
Además, el estudio ofrece una fórmula explícita para situaciones más generales, donde los estados no necesariamente son compatibles. Esto amplía el alcance del resultado y lo convierte en una herramienta más flexible para aplicaciones reales.
Qué cambia con esta nueva regla
En la versión cuántica de la regla de Bayes, el proceso es más complejo que en la versión clásica. Se parte de un estado inicial, representado por una matriz llamada gamma, y se aplica un canal cuántico que transforma ese estado. Luego, cuando se recibe nueva información, se busca un canal inverso que recupere la mayor parte posible del estado original.
Este canal inverso se calcula de manera que se maximice la fidelidad, es decir, la similitud entre el proceso directo (antes de actualizar) y el proceso inverso (tras recibir nueva información). Lo interesante es que este método funciona incluso cuando el nuevo dato no es una observación concreta, sino una distribución de probabilidades.
En este sentido, la propuesta del estudio se conecta con ideas más amplias de la teoría bayesiana y con el enfoque de retrodicción, que busca deducir el estado pasado a partir de los datos presentes. En física cuántica, donde el tiempo no siempre se comporta de forma clásica, este tipo de razonamientos cobra especial interés.
Futuras aplicaciones
Los autores del artículo destacan que esta nueva formulación puede tener impacto en varios campos. En primer lugar, en la computación cuántica, donde los sistemas son muy sensibles al ruido y a los errores. Una regla de actualización más precisa puede ayudar a mejorar los algoritmos de corrección de errores.
También tiene implicaciones en el aprendizaje automático cuántico, que se basa en ajustar modelos en entornos de alta incertidumbre. Si las probabilidades se pueden actualizar de forma más robusta, los sistemas podrán aprender mejor y con menos interferencia.
Otra línea de trabajo que se abre es la posibilidad de extender este principio de cambio mínimo a estructuras más complejas como las redes bayesianas cuánticas, los supermapas cuánticos o los llamados teoremas de fluctuación, que son fundamentales en termodinámica cuántica.
Referencias
- Ge Bai, Francesco Buscemi y Valerio Scarani. Quantum Bayes’ Rule and Petz Transpose Map from the Minimum Change Principle, Physical Review Letters, 28 de agosto de 2025. https://doi.org/10.1103/5n4p-bxhm.
Cortesía de Muy Interesante
Dejanos un comentario: