Los números de la sucesión de Fibonacci están presentes en espirales de caracolas, en la disposición de los pétalos de muchas flores y en la estructura de algunas galaxias. Su aparición repetida en fenómenos naturales ha convertido esta secuencia matemática en un símbolo de armonía. Ahora, un equipo internacional de investigadores ha encontrado un nuevo escenario para ella: el transporte controlado y robusto de luz a través de materiales diseñados especialmente para este propósito.
En un estudio publicado en eLight, los físicos liderados por Fangwei Ye, de la Universidad Jiao Tong de Shanghái, junto a colegas de Portugal y Rusia, demostraron experimentalmente que es posible “bombear” luz de forma controlada siguiendo patrones determinados por la sucesión de Fibonacci. El trabajo se apoya en un concepto de física conocido como bombeo topológico, que aprovecha propiedades globales del sistema para mover energía o partículas de manera precisa y resistente a perturbaciones. La novedad es que este bombeo no se realizó en un medio periódico, como se había hecho hasta ahora, sino en uno cuasiperiódico, lo que rompe un requisito considerado fundamental.
De un Nobel a un nuevo paradigma óptico
El bombeo topológico fue propuesto en 1983 por el Nobel David J. Thouless para explicar cómo electrones podían desplazarse de forma controlada en un potencial periódico modulado en el tiempo. Este mecanismo se caracteriza por depender de un invariante topológico —el número de Chern— y por ser resistente a defectos locales del medio. Según el artículo, se trata de un fenómeno “insensible a las imperfecciones locales del medio” y con aplicaciones en múltiples campos, desde la óptica hasta la acústica.
Hasta ahora, la investigación se había centrado en sistemas donde la modulación temporal era estrictamente periódica, lo que garantiza que el estado del sistema se repita cada cierto intervalo. El nuevo trabajo plantea una pregunta ambiciosa: ¿es posible mantener el bombeo topológico si esa periodicidad perfecta se rompe? El equipo exploró una configuración cuasiperiódica, modulando el sistema con dos frecuencias cuyo cociente es un número irracional. En este caso, eligieron el número áureo, estrechamente ligado a la sucesión de Fibonacci.
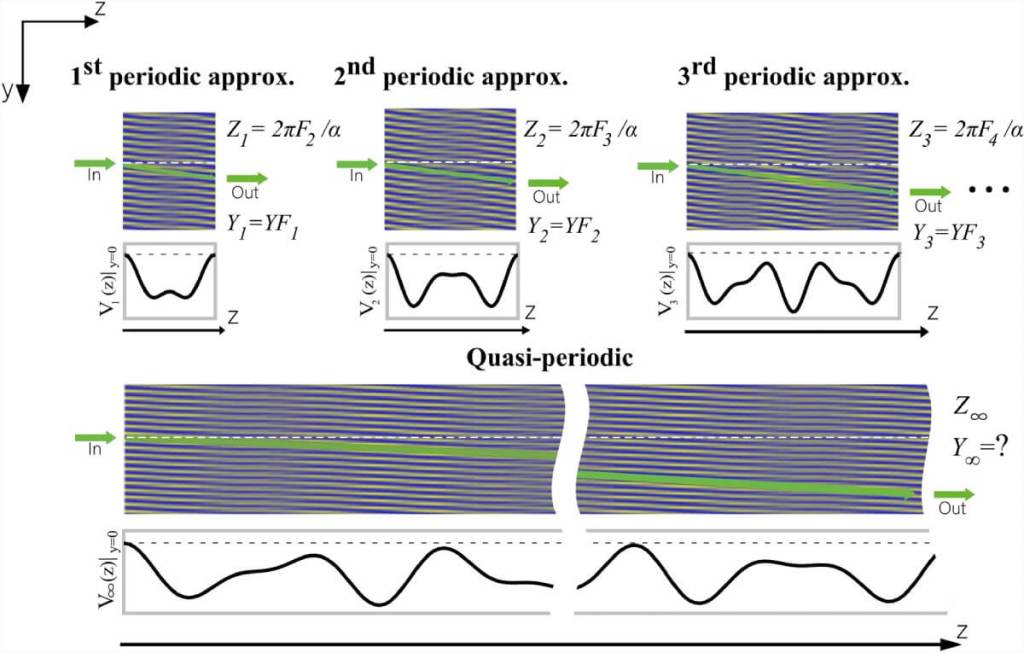
Cómo se conecta Fibonacci con el movimiento de la luz
Los autores recuerdan que cualquier número irracional puede aproximarse mediante fracciones compuestas por números enteros. En el caso del número áureo, esas fracciones se obtienen directamente de la sucesión de Fibonacci, donde cada término es la suma de los dos anteriores. Así, la relación entre dos frecuencias de modulación puede aproximarse progresivamente usando razones como 1/2, 2/3, 3/5, 5/8, y así sucesivamente.
En su experimento, esto se tradujo en una serie de “aproximantes periódicos” que imitan el comportamiento del sistema cuasiperiódico real. Estos aproximantes permitieron aplicar las herramientas teóricas del bombeo topológico convencional a un caso que, en principio, no cumple sus reglas. El hallazgo clave fue que los números de Cherncalculados para cada aproximante seguían exactamente la sucesión de Fibonacci: 1, 2, 3, 5, 8, 13… Tal como señalan, “el número de Chern para los sucesivos aproximantes coincide con los números de Fibonacci”, lo que determina directamente la velocidad a la que se transporta la luz.

Un montaje óptico para poner a prueba la teoría
El equipo trabajó con un cristal fotorefractivo de niobato de estroncio y bario (SBN) de 5×5×20 mm³. Usaron una técnica llamada inducción óptica, en la que haces láser ordinariamente polarizados interfieren para crear un patrón de refracción en el interior del cristal. Ese patrón actúa como una “red” que guía el haz de prueba, en este caso extraordinariamente polarizado, a lo largo del eje longitudinal.
Cada aproximante periódico requería un patrón ligeramente distinto, con periodos longitudinales relacionados según las razones de Fibonacci. En la práctica, la longitud del cristal solo permitió realizar los tres primeros aproximantes, con longitudes de media etapa de 8, 12 y 19 mm, respectivamente. En todos los casos, el equipo midió el desplazamiento lateral del centro de masa del haz tras recorrer medio ciclo de bombeo.

Resultados: la huella de Fibonacci en el desplazamiento
Las mediciones experimentales mostraron un desplazamiento del haz que coincidía con las predicciones teóricas para cada aproximante, siguiendo la regla de Fibonacci. Incluso al variar de forma considerable la amplitud de la red mediante cambios de voltaje, la velocidad de bombeo permaneció prácticamente constante. Esto confirma que la robustez topológica se mantiene en el régimen cuasiperiódico.
El artículo explica que “la velocidad del bombeo está determinada por las propiedades topológicas globales de las bandas” y no por imperfecciones locales o desorden. Además, las simulaciones numéricas reprodujeron el comportamiento observado, incluyendo la convergencia de la velocidad media hacia el valor límite determinado por el número áureo.
Qué significa para la física y la tecnología
Este trabajo demuestra que no es necesaria la estricta periodicidad temporal para lograr bombeo topológico, lo que amplía de forma notable las posibilidades de diseño en sistemas fotónicos y otros medios ondulatorios. La estrategia de usar aproximantes periódicos para describir un sistema cuasiperiódico abre también la puerta a explorar otros números irracionales distintos del áureo.
Los autores sugieren que el concepto podría aplicarse en ámbitos como los átomos ultrafríos, la plasmonónica o los sistemas acústicos, donde se pueden implementar modulaciones cuasiperiódicas. También señalan que la plataforma experimental utilizada permite investigar interacciones entre topología, simetría y no linealidad, con potencial para descubrir nuevos estados de la materia y diseñar dispositivos cuánticos con propiedades de transporte únicas.
Retos y futuras direcciones
A pesar de su éxito, los experimentos se enfrentaron a un desafío notable: la difracción del haz durante el bombeo, que se acentúa en aproximantes de orden más alto. Reducir este efecto requeriría aumentar la profundidad de la red, algo limitado por la técnica de inducción óptica. Entre las posibles soluciones están el uso de arreglos de guías de onda discretas, que permiten mayor confinamiento, o la explotación de efectos no lineales para mantener la localización del haz.
Otra vía de investigación será llevar este bombeo cuasiperiódico a sistemas bidimensionales, como redes fotónicas tipo moiré, donde la difracción puede controlarse mejor. Este tipo de configuraciones podría revelar comportamientos de transporte aún más complejos y robustos.
Más allá de la óptica
La demostración de que la sucesión de Fibonacci puede guiar el transporte de luz no es solo un hallazgo curioso: es una prueba de que las leyes matemáticas que rigen la naturaleza pueden aprovecharse para controlar el movimiento de energía de forma predecible y resistente. El hecho de que un patrón numérico presente en flores y galaxias pueda encontrar aplicación en tecnologías de manipulación de la luz ilustra la conexión profunda entre matemáticas y física experimental.
Como concluyen los autores, la estrategia de aproximar un sistema cuasiperiódico mediante secuencias periódicas “permite observar una transición relativamente rápida hacia la velocidad media de bombeo, confirmando su origen topológico”. En otras palabras, la luz sigue las reglas de Fibonacci incluso en un entorno que rompe las normas clásicas del bombeo topológico.
Referencias
- Ruihan Peng, Kai Yang, Qidong Fu, Yanli Chen, Peng Wang, Yaroslav V. Kartashov, Vladimir V. Konotop, Fangwei Ye. Topological pumping of light governed by Fibonacci numbers. eLight (2025) 5:16. https://doi.org/10.1186/s43593-025-00095-9.
Cortesía de Muy Interesante
Dejanos un comentario:

